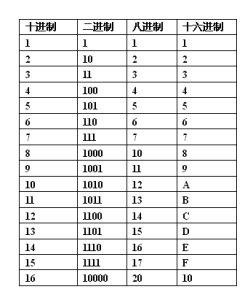
簡介
二,十進制轉換為八進制常見方法
抽象的二進制加法：0+0=0，0+1=1，1+0=1，1+1=10
減法：0－0=0，1－0=1，1－1=0，0－1=1
乘法：0×0=0，0×1=0，1×0=0，1×1=1
除法：0÷1=0，1÷1=1, 1÷0無意義,0÷0無意義
相關轉換
二進制轉換
二進制數第0位的權值是2的0次方，第1位的權值是2的1次方。
例如，設有一個二進制數：0110 0100（由後至前分別為第0位，第1位……第7位），轉換為10進制為：
下面是豎式：
01100 100 換算成 十進制
第0位 0 x 2^0 = 0
第1位 0 x 2^1 = 0
第2位 1 x 2^2 = 4
第3位 0 x 2^3 = 0
第4位 0 x 2^4 = 0
第5位 1 x 2^5 = 32
第6位 1 x 2^6 = 64
第7位 0 x 2^7 = 0
--------------------------
(01100 100)B=(100)D
註：數字後面相應的字母表示不同的進位制。B表示二進制,O表示八進制，D表示十進制，H表示十六進制。
八進制轉換
八進制就是逢8進1。
八進制數採用 0～7這八數來表達一個數。
八進制數第0位的權值為8的0次方，第1位權值為8的1次方，第2位權值為8的2次方……
所以，設有一個八進制數：1507，轉換為十進制為：
用豎式表示：
1507換算成十進制。
第0位 7 x 8^0 = 7
第1位 0 x 8^1 = 0
第2位 5 x 8^2 = 320
第3位 1 x 8^3 = 512
--------------------------
(1507)O=(839)D
同樣，我們也可以用橫式直接計算：
7 X 8^0 + 0 X 8^1 + 5 X 8^2 + 1 x 8^3 = (839)D
結果是，八進制數1507 轉換成十進制數為 839
十六進制轉換為十進制
(ABC.8C)H=10x16^2+11x16^1+12x16^0+8x16^-1+12x16^-2
=2560+176+12+0.5+0.046875
=(2748.546875)D
十進制轉換
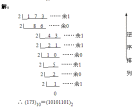
1.整數部分除R取余
例：(125)D=(1111101)B
註：餘數中最後得到的餘數為最高位，最先得到的餘數為最低位，從高到低依次排列。
2.小數部分乘R取整
例：(0.25)D
0.25
X 2
_______________
0.50 （整數部分0為高位）
X 2 ↓
_______________ ↓
1.00 （整數部分1為低位）
(0.25)D=(0.01)B
註：整數的轉換是精確的，小數的轉換可能出現無窮小數或循環小數的情況。此時需要進行捨入處理以截斷，所以小數的轉換可能略有偏差。箭頭表示由高位到低位的趨勢。
