主要問題
假設字長為8bits要完成,1-1=0
(1)-(1)
=(1)+(-1)
=(00000001)+(10000001)-----------------原碼計算
 碼
碼=(10000010)=(-2)
(1)-(2)
=(1)+(-2)
=(00000001)+(10000010)-----------------原碼計算
=(10000011)=(-3)
顯然結果不正確.
因為在兩個整數的加法運算中是沒有問題的,於是就發現問題出現在帶符號位的負數身上,對除符號位外的其餘各位逐位取反就產生了反碼.反碼的取值空間和原碼相同且一一對應.
下面是反碼的減法運算:
(1)+(-1)
=(00000001)+(11111110)----反碼計算
=(11111111)
=(10000000)
=(-0)有問題
按上面同樣的方法計算1-2=-1
1+(-2)
=(00000001)+(11111101)----反碼計算
=(11111110)
=(10000001)=(-1)正確
問題出現在(+0)和(-0)上,在人們的計算概念中零是沒有正負之分的.(印度人首先將零作為標記並放入運算之中,包含有零號的印度數學和十進制計數對人類文明的貢獻極大).於是就引入了補碼概念.
負數的補碼
負數的補碼就是對反碼加1,而正數不變,正數的原碼反碼補碼是一樣的.
1.補碼的得來:是為了讓負數變成能夠加的正數,so,負數的補碼=模-負數的絕對值比如:-1補碼:11111111(100000000-1得來)
當一個數要減1的時候,可以直接加11111111
2.原碼的得來:(負數的原碼,直接把對應正數的最高位改為1)
原碼能夠直觀的表示一個負數(能直觀的把真值顯示出來,如-1為10000001
其中最高位表示符號位,不進行算術計算)
3.原碼和補碼之間轉換:補碼=反碼+1
4.現在來推-128的補碼:
-128的補碼:100000000-10000000(+128沒有符號位)=10000000
-128的反碼:11111111(10000000-1=10000000+11111111=11111111)
-128的原碼:10000000(反碼取反)
往回推:
-128的原碼10000000(-128,進位被捨去)
-128的反碼11111111
-128的補碼10000000(11111111(反碼)+1=10000000,這裡實際上真正相加的是
11111111後面的7位,第1位是符號位始終不會變,
所以,當進到第8位的時候,就表示溢出了,會被捨棄)
5.0隻有一個補碼00000000(聽說可以證明的),如果是這樣,那么10000000就不會表示成-0的補碼
即:補碼10000000唯一的表示-128
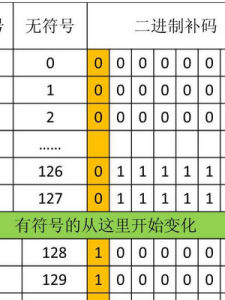
在補碼中用(-128)代替了(-0),所以補碼的表示範圍為:(-128~0~127)共256個.
注意:(-128)也有相對應的原碼和反碼,它的反碼是(11111111)原碼仍然是(10000000)(-128)
補碼的加減運算如下:
下面是補碼的運算:
(1)-(1)=(1)+(-1)
=(00000001)補+(11111111)補((11111110)+1)(反碼加1)
=(00000000)補=(0)正確
(1)-(2)=(1)+(-2)
=(00000001)補+(11111110)補
=(11111111)補=(-1)正確
(-1)=(10000001)原碼=(11111110)反碼=((11111110)+1)補碼
設計目的
所以補碼的設計目的是:⑴使符號位能與有效值部分一起參加運算,從而簡化運算規則.
⑵使減法運算轉換為加法運算,進一步簡化計算機中運算器的線路設計所有這些轉換都是在計算機的最底層進行的,而在我們使用的彙編、C等其他高級語言中使用的都是原碼。
小數和分數的補碼
一、十進制分數補碼可以先將分子和分母分別表示成二進制數,然後計算出二進制小數,再按下面第三步的方法將求出小數的補碼形式。
37/64=100101B/2^6=0.100101B
-51/128=110011B/2^7=0.0110011B
二、十進制小數的補碼也應該先將其轉換成二進制小數,再按下面第三步的方法將求出小數的補碼形式。
0.375=0.011B
0.5625=0.1001B
三、將二進制小數對應的補碼求出
[37/64]補碼=[0.100101B]補碼=01001010B
[-51/128]補碼=[0.0110011B]補碼=11001101B
[0.375]補碼=[0.011B]補碼=00110000B
[0.5625]補碼=[0.1001B]補碼=01001000B
