數制簡介
二進制
 十進制轉二進制
十進制轉二進制20世紀被稱作第三次科技革命的重要標誌之一的計算機的發明與套用,其運算模式正是二進制,二進制是計算技術中廣泛採用的一種數制。二進制數據是用0和1兩個數碼來表示的數。它的基數為2,進位規則是“逢二進一”,借位規則是“借一當二”,由18世紀德國數理哲學大師萊布尼茲發現。當前的計算機系統使用的基本上是二進制系統。
十進制
十進制計數法是相對二進制計數法而言的,是我們日常使用最多的計數方法(俗稱“逢十進一”),它的定義是:“每相鄰的兩個計數單位之間的進率都是十”的計數方法,叫做“十進制計數法”。
二進制轉十進制
要從右到左用二進制的每個數去乘以2的相應次方
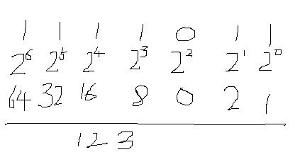
例如:二進制數1101.01轉化成十進制
1101.01(2)=1*2+0*2+1*2+1*2+0*2+1*2=1+0+4+8+0+0.25=13.25
所以總結起來通用公式為:
abcd.efg(2)=d*2+c*2+b*2+a*2+e*2+f*2+g*2
或者用下面這種方法:
把二進制數首先寫成加權係數展開式,然後按十進制加法規則求和。這種做法稱為"按權相加"法。
2的0次方是1(任何數的0次方都是1,0的0次方無意義)
2的1次方是2
2的2次方是4
2的3次方是8
2的4次方是16
2的5次方是32
2的6次方是64
2的7次方是128
2的8次方是256
2的9次方是512
2的10次方是1024
2的11次方是2048
2的12次方是4096
2的13次方是8192
2的14次方是16384
2的15次方是32768
2的16次方是65536
2的17次方是131072
2的18次方是262144
2的19次方是524288
2的20次方是1048576
即:
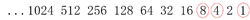 十進制轉二進制
十進制轉二進制此時,1101=8+4+0+1=13
再比如:二進制數1000110轉成十進制數可以看作這樣:
數字中共有三個1 即第二位一個,第三位一個,第七位一個,然後對應十進制數即2的1次方+2的2次方+2的6次方, 即
1000110=64+0+0+0+4+2+0=70
十進制轉二進制
 十進制轉二進制
十進制轉二進制1. 十進制整數轉換為二進制整數
十進制整數轉換為二進制整數採用"除2取余,逆序排列"法。具體做法是:用2整除十進制整數,可以得到一個商和餘數;再用2去除商,又會得到一個商和餘數,如此進行,直到商為0時為止,然後把先得到的餘數作為二進制數的低位有效位,後得到的餘數作為二進制數的高位有效位,依次排列起來。
十進制整數轉二進制
如:255=(11111111)B
255/2=127=====餘1
127/2=63======餘1
63/2=31=======餘1
31/2=15=======餘1
15/2=7========餘1
7/2=3=========餘1
3/2=1=========餘1
1/2=0=========餘1
789=1100010101
789/2=394 餘1 第10位
394/2=197 餘0 第9位
197/2=98 餘1 第8位
98/2=49 餘0 第7位
49/2=24 餘1 第6位
24/2=12 餘0 第5位
12/2=6 餘0 第4位
6/2=3 餘0 第3位
3/2=1 餘1 第2位
1/2得0 餘1 第1位
原理:
眾所周知,二進制的基數為2,我們十進制化二進制時所除的2就是它的基數。談到它的原理,就不得不說說關於位權的概念。某進制計數制中各位數字元號所表示的數值表示該數字元號值乘以一個與數字元號有關的常數,該常數稱為 “位權 ” 。位權的大小是以基數為底,數字元號所處的位置的序號為指數的整數次冪。十進制數的百位、十位、個位、十分位的權分別是10的2次方、10的1次方、10的0次方,10的-1次方。二進制數就是2的n次冪。
按權展開求和正是非十進制化十進制的方法。
下面我們開講原理,舉個十進制整數轉換為二進制整數的例子,假設十進制整數A化得的二進制數為edcba 的形式,那么用上面的方法按權展開, 得
A=a(2^0)+b(2^1)+c(2^2)+d(2^3)+e(2^4) (後面的和不正是化十進制的過程嗎)
假設該數未轉化為二進制,除以基數2得
A/2=a(2^0)/2+b(2^1)/2+c(2^2)/2+d(2^3)/2+e(2^4)/2
注意:a除不開二,餘下了!其他的絕對能除開,因為他們都包含2,而a乘的是1,他本身絕對不包含因數2,只能餘下。
商得:
b(2^0)+c(2^1)+d(2^2)+e(2^3),再除以基數2餘下了b,以此類推。
當這個數不能再被2除時,先余掉的a位數在原數低,而後來的餘數數位高,所以要把所有的餘數反過來寫。正好是edcba
2.十進制小數轉換為二進制小數
十進制小數轉換成二進制小數採用"乘2取整,順序排列"法。具體做法是:用2乘十進制小數,可以得到積,將積的整數部分取出,再用2乘餘下的小數部分,又得到一個積,再將積的整數部分取出,如此進行,直到積中的小數部分為零,此時0或1為二進制的最後一位。或者達到所要求的精度為止。
然後把取出的整數部分按順序排列起來,先取的整數作為二進制小數的高位有效位,後取的整數作為低位有效位。
十進制小數轉二進制
如:0.625=(0.101)B
0.625*2=1.25======取出整數部分1
0.25*2=0.5========取出整數部分0
0.5*2=1==========取出整數部分1
再如:0.7=(0.1 0110 0110...)B
0.7*2=1.4========取出整數部分1
0.4*2=0.8========取出整數部分0
0.8*2=1.6========取出整數部分1
0.6*2=1.2========取出整數部分1
0.2*2=0.4========取出整數部分0
0.4*2=0.8========取出整數部分0
0.8*2=1.6========取出整數部分1
0.6*2=1.2========取出整數部分1
0.2*2=0.4========取出整數部分0
原理:
關於十進制小數轉換為二進制小數
假設一十進制小數B化為了二進制小數0.ab的形式,同樣按權展開,得
B=a(2^-1)+b(2^-2)
因為小數部分的位權是負次冪,所以我們只能乘2,得
2B=a+b(2^-1)
注意a變成了整數部分,我們取整數正好是取到了a,剩下的小數部分也如此。
值得一提的是,小數部分的按權展開的數位順數正好和整數部分相反,所以不必反向取餘數了。
十進制轉二進制C++代碼

