二進制編碼輸出

二進制編碼輸出是指將文字、符號或十進制數等特定的信息通過二進制編碼轉換成二進制數碼輸出，可通過編碼器實現。典型的編碼器有二進制編碼器、二-十進制編碼器等。

編碼

由於數字電路只能以二進制信號工作，因此，需將將生活中常用的十進制數、文字或符號等對象表示成特定對象，這個過程就是編碼。例如，學生的學號、各地郵政編碼、公車車號等。

用二進制數進行編碼，稱為二進制編碼，相應的二進制數叫做二進制代碼。

編碼器

編碼器是指能將每一組輸入信息或數目變換為相應二進碼輸出，即能完成特定編碼功能的邏輯電路。常用的編碼器有二進制編碼器、二-十進制編碼器、優先編碼器等。

二進制編碼器

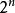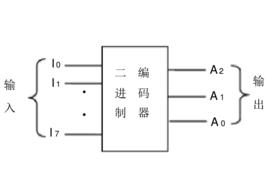
二進制編碼輸出

用n位二進制代碼對 個信號進行編碼的電路，稱為二進制編碼器。常用的二進制編碼器有 4 線-2 線、 8 線-3 線和 16 線-4 線等。

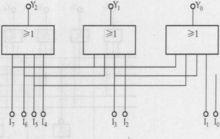圖1 3位二進制編碼器邏輯電路

二進制編碼輸出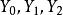

二進制編碼輸出

由於編碼器各個輸出信號邏輯表達式的基本形式是有關輸入信號的或運算，所以其邏輯電路是由或門組成的陣列，這也是編碼器基本電路結構的一個顯著特點。圖 1是8 線-3 線編碼器的框圖，其中， 表示輸入信號， 表示輸出信號。對於3位二進制編碼器，由於任何時刻只對其中一個輸入信號進行編碼，即輸入的信號I、I、…、I是互相排斥的。假設輸入高電平有效，則任何時刻只允許一個端子為 1，其餘均為 0。所以只需要將使函式值為1的變數加起來，便可以得到相應輸出信號的最簡與或表達式，即：

Y=I+I+I+I

Y=I+I+I+I

Y=I+I+I+I

其真值表如下表所示：

輸入								輸出
I	I	I	I	I	I	I	I	Y	Y	Y
1	0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	0	0	0	1	0
0	0	0	1	0	0	0	0	0	1	1
0	0	0	0	1	0	0	0	1	0	0
0	0	0	0	0	1	0	0	1	0	1
0	0	0	0	0	0	1	0	1	1	0
0	0	0	0	0	0	0	1	1	1	1

二-十進制編碼器

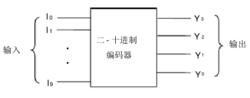圖2 二- 十進制編碼器框圖

二- 十進制編碼器是指能實現二—十進制編碼的電路，即用四位二進制代碼表示一位十進制數（ 0～9）的編碼電路，也稱 10 線4線編碼器。它有 10 個信號輸入端和 4 個輸出端。圖 2是二- 十進制編碼器框圖。

常用的編碼，二—十進制編碼有8421碼、餘3碼、2421碼、5211碼、餘3循環碼、右移循環碼，還有循環碼、ISO編碼、ANSCⅡ (ASC Ⅱ)碼等。

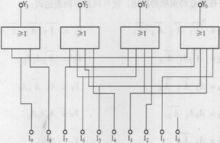圖3 8421 BCD編碼器邏輯電路

二—十進制編碼器的工作原理與二進制編碼器類同，以8421BCD碼編碼器為例，其邏輯電路如圖3所示，I～I是一組互相排斥的變數，其邏輯表達式，即直接寫出每一個輸出信號的最簡與或表達式，為：

Y=I+I

Y=I+I+I+I

Y=I+I+I+I

Y=I+I+I+I+I

其真值表如下表所示：

輸入										輸出
I	I	I	I	I	I	I	I	I	I	Y	Y	Y	Y
1	0	0	0	0	0	0	0	0	0	0	0	0	0
0	1	0	0	0	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	0	0	0	0	0	0	1	0
0	0	0	1	0	0	0	0	0	0	0	0	1	1
0	0	0	0	1	0	0	0	0	0	0	1	0	0
0	0	0	0	0	1	0	0	0	0	0	1	0	1
0	0	0	0	0	0	1	0	0	0	0	1	1	0
0	0	0	0	0	0	0	1	0	0	0	1	1	1
0	0	0	0	0	0	0	0	1	0	1	0	0	0
0	0	0	0	0	0	0	0	0	1	1	0	0	1