算法介紹
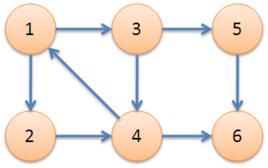
如果兩個頂點可以相互通達，則稱兩個頂點 強連通(strongly connected)。如果有向圖G的每兩個頂點都強連通，稱G是一個 強連通圖。有向圖的極大強連通子圖，稱為 強連通分量(strongly connected components)。
下圖中，子圖{1,2,3,4}為一個強連通分量，因為頂點1,2,3,4兩兩可達。{5},{6}也分別是兩個強連通分量。
Tarjan算法是用來求有向圖的強連通分量的。求有向圖的強連通分量的Tarjan算法是以其發明者Robert Tarjan命名的。Robert Tarjan還發明了求雙連通分量的Tarjan算法。
Tarjan算法是基於對圖深度優先搜尋的算法，每個強連通分量為搜尋樹中的一棵子樹。搜尋時，把當前搜尋樹中未處理的節點加入一個堆疊，回溯時可以判斷棧頂到棧中的節點是否為一個強連通分量。
定義DFN(u)為節點u搜尋的次序編號(時間戳)，Low(u)為u或u的子樹能夠追溯到的最早的棧中節點的次序號。
當DFN(u)=Low(u)時，以u為根的搜尋子樹上所有節點是一個強連通分量。
接下來是對算法流程的演示。
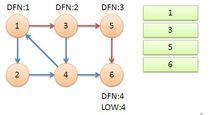
從節點1開始DFS，把遍歷到的節點加入棧中。搜尋到節點u=6時，DFN[6]=LOW[6]，找到了一個強連通分量。退棧到u=v為止，{6}為一個強連通分量。
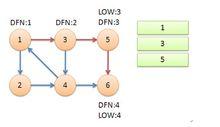
tarjan算法返回節點5，發現DFN[5]=LOW[5]，退棧後{5}為一個強連通分量。
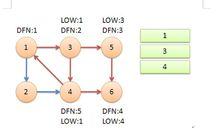
tarjan算法返回節點3，繼續搜尋到節點4，把4加入堆疊。發現節點4向節點1有後向邊，節點1還在棧中，所以LOW[4]=1。節點6已經出棧，(4,6)是橫叉邊，返回3，(3,4)為樹枝邊，所以LOW[3]=LOW[4]=1。
tarjan算法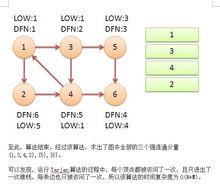
tarjan算法繼續回到節點1，最後訪問節點2。訪問邊(2,4)，4還在棧中，所以LOW[2]=DFN[4]=5。返回1後，發現DFN[1]=LOW[1]，把棧中節點全部取出，組成一個連通分量{1,3,4,2}。
至此，算法結束。經過該算法，求出了圖中全部的三個強連通分量{1,3,4,2},{5},{6}。
可以發現，運行Tarjan算法的過程中，每個頂點都被訪問了一次，且只進出了一次堆疊，每條邊也只被訪問了一次，所以該算法的時間複雜度為O(N+M)。
