概念
強連通簡介
在計算機圖論中,強連通(Strongly Connected)是指有向圖G(Directed Graph)中任意兩點v1、v2之間都存在著v1到v2的路徑(path,若途徑的點和邊都不重複,則稱為路徑)及v2到v1的路徑。
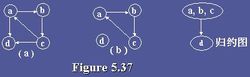 強連通
強連通定理:
一個有向圖是強連通的,若且唯若G中有一個迴路,它至少包含每個節點一次。
證明:
充分性
如果G中有一個迴路,它至少包含每個節點一次,則G中任兩個節點都是互相可達的,故G是強連通圖。
必要性
如果有向圖是強連通的,則任兩個節點都是相互可達。故必可做一迴路經過圖中所有各點。若不然則必有一迴路不包含某一結點v,並且v與迴路上的個節點就不是相互可達,與強連通條件矛盾。
有向圖強連通分量
在有向圖G中,如果兩個頂點間至少存在一條路徑,稱兩個頂點強連通(strongly connected)。如果有向圖G的每兩個頂點都強連通,稱G是一個強連通圖。非強連通圖有向圖的極大強連通子圖,稱為強連通分量(strongly connected components)。
算法
直接根據定義,用雙向遍歷取交集的方法求強連通分量,時間複雜度為O(N^2+M)。更好的方法是Kosaraju算法或Tarjan算法,兩者的時間複雜度都是O(N+M)。本文介紹的是Tarjan算法。
強連通分量的Tarjan算法
Tarjan算法是基於對圖深度優先搜尋的算法,每個強連通分量為搜尋樹中的一棵子樹。搜尋時,把當前搜尋樹中未處理的節點加入一個堆疊,回溯時可以判斷棧頂到棧中的節點是否為一個強連通分量。
定義DFN(u)為節點u搜尋的次序編號(時間戳),Low(u)為u或u的子樹能夠追溯到的最早的棧中節點的次序號。由定義可以得出,
Low(u)=Min{DFN(u),Low(v),(u,v)為樹枝邊,u為v的父節點
DFN(v),(u,v)為指向棧中節點的後向邊(非橫叉邊)}
當DFN(u)=Low(u)時,以u為根的搜尋子樹上所有節點是一個強連通分量。
算法偽代碼如下
tarjan(u)
{
DFN[u]=Low[u]=++Index // 設定次序編號和Low初值
Stack.push(u) // 將節點u壓入棧中
for each (u, v) in E // 枚舉每一條邊
if (v is not visted) // 如果節點v未被訪問過
tarjan(v) // 繼續向下找
Low[u] = min(Low[u], Low[v])
else if (v in S) // 如果節點v還在棧內
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果節點u是強連通分量的根
repeat
v = S.pop // 將v退棧,為該強連通分量中一個頂點
print v
until (u== v)
}
接下來是對算法流程的演示。
從節點1開始DFS,把遍歷到的節點加入棧中。搜尋到節點u=6時,DFN=LOW,找到了一個強連通分量。退棧到u=v為止,{6}為一個強連通分量。
返回節點5,發現DFN=LOW,退棧後{5}為一個強連通分量。
返回節點3,繼續搜尋到節點4,把4加入堆疊。發現節點4像節點1的後向邊,節點1還在棧中,所以LOW=1。節點6已經出棧,不再訪問6,返回3,(3,4)為樹枝邊,所以LOW=LOW=1。
繼續回到節點1,最後訪問節點2。訪問邊(2,4),4還在棧中,所以LOW=4。返回1後,發現DFN=LOW,把棧中節點全部取出,組成一個連通分量{1,3,4,2}。
至此,算法結束。經過該算法,求出了圖中全部的三個強連通分量{1,3,4,2},{5},{6}。
可以發現,運行Tarjan算法的過程中,每個頂點都被訪問了一次,且只進出了一次堆疊,每條邊也只被訪問了一次,所以該算法的時間複雜度為O(N+M)。
求有向圖的強連通分量還有一個強有力的算法,為Kosaraju算法。Kosaraju是基於對有向圖及其逆圖兩次DFS的方法,其時間複雜度也是 O(N+M)。與Trajan算法相比,Kosaraju算法可能會稍微更直觀一些。但是Tarjan只用對原圖進行一次DFS,不用建立逆圖,更簡潔。 在實際的測試中,Tarjan算法的運行效率也比Kosaraju算法高30%左右。此外,該Tarjan算法與求無向圖的雙連通分量(割點、橋)的Tarjan算法也有著很深的聯繫。學習該Tarjan算法,也有助於深入理解求雙連通分量的Tarjan算法,兩者可以類比、組合理解。
雙連通分量的Tarjan算法
求有向圖的強連通分量的Tarjan算法是以其發明者Robert Tarjan命名的。Robert Tarjan還發明了求雙連通分量的Tarjan算法,以及求最近公共祖先的離線Tarjan算法,在此對Tarjan表示崇高的敬意。
void tarjan(int i)
{
int j;
DFN[i]=LOW[i]=++Dindex;
instack[i]=true;
Stap[++Stop]=i;
for (edge *e=V[i];e;e=e->next)
{
j=e->t;
if (!DFN[j])
{
tarjan(j);
if (LOW[j]
LOW[i]=LOW[j];
}
else if (instack[j] && DFN[j]
LOW[i]=DFN[j];
}
if (DFN[i]==LOW[i])
{
Bcnt++;
do
{
j=Stap[Stop--];
instack[j]=false;
Belong[j]=Bcnt;
}
while (j!=i);
}
}
void solve()
{
int i;
Stop=Bcnt=Dindex=0;
memset(DFN,0,sizeof(DFN));
for (i=1;i<=N;i++)
if (!DFN[i])
tarjan(i);
}
連通圖
在圖論中,連通圖基於連通的概念。在一個無向圖 G 中,若從頂點vi到頂點vj有路徑相連(當然從vj到vi也一定有路徑),則稱vi和vj是連通的。如果 G 是有向圖,那么連線vi和vj的路徑中所有的邊都必須同向。如果圖中任意兩點都是連通的,那么圖被稱作連通圖。如果此圖是有向圖,則稱為強連通圖(注意:需要雙向都有路徑)。圖的連通性是圖的基本性質。
強連通圖和弱連通圖
強連通圖:在有向圖中, 若對於每一對頂點v1和v2, 都存在一條從v1到v2和從v2到v1的路徑,則稱此圖是強連通圖。
弱連通圖:將有向圖的所有的有向邊替換為無向邊,所得到的圖稱為原圖的基圖。如果一個有向圖的基圖是連通圖,則有向圖是弱連通圖。