基本介紹
 平面性算法
平面性算法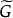 平面性算法
平面性算法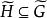 平面性算法
平面性算法 平面性算法
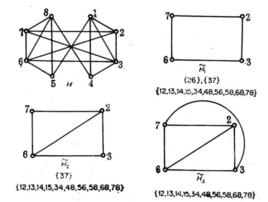
平面性算法平面性算法(planarity algorithm)是一種求 平面嵌入的算法,指判斷一個給定的圖是否是可平面圖,並且如果它是可平面圖,則要找出它的平面嵌入來。設H是圖G的一個可平面子圖, 是H在這個平面中的一個嵌入,若G是可平面圖,且存在G的一個平面嵌入 ,使得 ,則稱 是G 容許的。例如,圖1表示G的一個平面子圖的兩個嵌人;一個是G容許的,而另一個則不是。
 圖1(a) G
圖1(a) G 圖1(b) G容許的嵌入
圖1(b) G容許的嵌入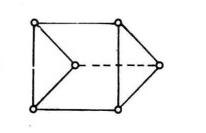 圖1(c) G不容許的嵌入
圖1(c) G不容許的嵌入 平面性算法
平面性算法 平面性算法
平面性算法 平面性算法
平面性算法 平面性算法
平面性算法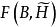 平面性算法
平面性算法 平面性算法
平面性算法若B是H(在G中)的任意一座橋,且B對於H的接觸點都包含在 的面 的周界上,則稱B在 的面 內是 可畫的。用 表示在 中橋B是可畫出的那些面的集。
相關定理
平面性算法是基於如下定理:
 平面性算法
平面性算法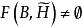 平面性算法
平面性算法若 是容許的,則對於H的每座橋B, 。
 平面性算法
平面性算法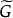 平面性算法
平面性算法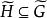 平面性算法
平面性算法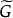 平面性算法
平面性算法 平面性算法
平面性算法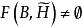 平面性算法
平面性算法證明:若 是G容許的,則根據定義,存在G的一個平面嵌入 ,使得 。顯然,H的橋B所對應的 的子圖必然限制在 的一個面中,因此 。
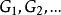 平面性算法
平面性算法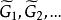 平面性算法
平面性算法由於一個圖是平面圖若且唯若它的基礎簡單圖的每個塊都是平面圖,所以只要考察簡單塊就夠了。給定這樣的一個圖G後。算法就確定了G的一個平面子圖的遞增序列 ,以及對應的平面嵌入 ,終止於G的一個平面嵌入。對每一步,都套用定理的必要條件,來判斷G的非平面性 。
具體過程
步驟如下:
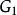 平面性算法
平面性算法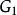 平面性算法
平面性算法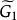 平面性算法
平面性算法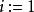 平面性算法
平面性算法1.設 是G的一個圈,找出 的一個平面嵌入 ,置 ;
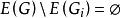 平面性算法
平面性算法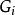 平面性算法
平面性算法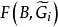 平面性算法
平面性算法2.若 ,則停止;否則,確定G中 的所有橋;對於每座這樣的橋B,找出集 ;
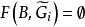 平面性算法
平面性算法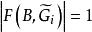 平面性算法
平面性算法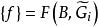 平面性算法
平面性算法 平面性算法
平面性算法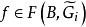 平面性算法
平面性算法3.若存在一座橋B,使得 ,則停止,根據定理,G是非平面圖,若存在一座橋B,使得 ,則令 ,否則令B是任一座橋,且 是任一使得 的面;
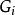 平面性算法
平面性算法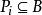 平面性算法
平面性算法 平面性算法
平面性算法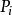 平面性算法
平面性算法 平面性算法
平面性算法 平面性算法
平面性算法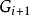 平面性算法
平面性算法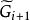 平面性算法
平面性算法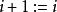 平面性算法
平面性算法4.選擇一條連結B對於 的兩個接觸頂點的路 ,置 ,並把 畫在 的面 內,得到 的一個平面嵌 ,令 ,轉入步驟2。
這個算法是一個有效算法,它的主要運算包括:
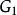 平面性算法
平面性算法(i) 找出圖G中的一個圈 ;
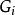 平面性算法
平面性算法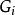 平面性算法
平面性算法(ii) 確定G中 的橋以及它們對於 的接觸頂點;
 平面性算法
平面性算法 平面性算法
平面性算法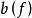 平面性算法
平面性算法(iii) 對於 的每個面 確定 ;
 平面性算法
平面性算法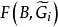 平面性算法
平面性算法(iv) 對於 的每座橋B,確定 ;
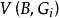 平面性算法
平面性算法(v) 在G的某座橋B中求 的兩個頂點之間的一條路P;
上述每一個運算都存在有效算法,因此,這個算法是一個有效算法。繼這個方法之後,許多研究者都致力於這種平面性算法的研究並提出了一些算法。
套用舉例
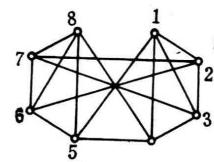 圖2 G
圖2 G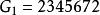 平面性算法
平面性算法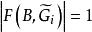 平面性算法
平面性算法 平面性算法
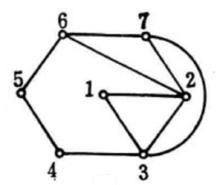
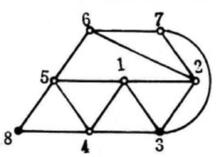
平面性算法為了說明這個算法,考察圖2中的圖G,從圈 和G的一張橋的表開始(為了簡潔起見,橋用其邊集來表示);在每一步中。對於 的橋B以粗體字標出。這個例子中,算法終止於G的一個平面嵌入 ,所以G是平面圖。
 平面性算法 平面性算法  平面性算法 平面性算法 | 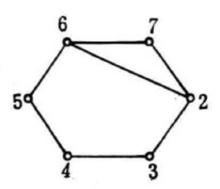 平面性算法 平面性算法  平面性算法 平面性算法 | 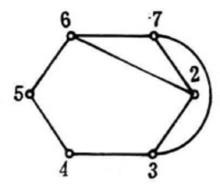 平面性算法 平面性算法 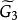 平面性算法 平面性算法 |
 平面性算法 平面性算法 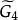 平面性算法 平面性算法 |  平面性算法 平面性算法  平面性算法 平面性算法 |  平面性算法 平面性算法 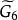 平面性算法 平面性算法 |
 平面性算法 平面性算法  平面性算法 平面性算法 |  平面性算法 平面性算法 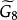 平面性算法 平面性算法 | 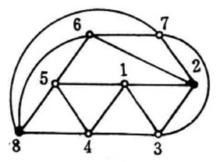 平面性算法 平面性算法  平面性算法 平面性算法 |