簡歷
Robert Tarjan他還在多所大學擔任學術職務,如:康奈爾大學(1972-1973年),加州大學伯克利分校(1973-1975),史丹福大學(1974-1980),紐約大學(1981-1985)。 他也加入過NEC研究所(1989-1997),並在美國麻省理工學院(1996年)擔任Visiting Scientist 。
Tarjan:他曾在AT&T貝爾實驗室(1980-1989),浩信科技(1997-2001),康柏(2002年)和惠普(2006年至今)工作。 他曾加入ACM和IEEE委員會,並曾為幾家期刊的編輯。
早期生活
Robert Tarjan出生在波莫納,加利福尼亞州。他的父親是一個專業兒童精神科醫生,以前在國家醫院任職。還是孩子的Robert Tarjan就閱讀了大量的科學小說,從此對天文學產生興趣,並夢想成為一名天文學家。他在Scientific American雜誌上看完 Martin Gardner的數學遊戲後又對數學產生了興趣。他的一位中學老師發現了他對數學的興趣,從八年級就開始培育他的數學能力。之後Robert開始深入研究數學。
Robert Tarjan上高中就找到了一份工作:從事IBM卡片校對機的工作。 他第一次真正用計算機工作是在1964年,那時他參與Summer Science Program在其中研究天文學。
Robert Tarjan在1969年獲得了加州理工學院數學學士學位。在史丹福大學,他獲得了他的計算機科學碩士學位(1971)和博士學位(1972)。在斯坦福,他由羅伯特·弗洛伊德和高德納指導,兩位都是非常突出的計算機科學家。他的博士論文是 An Efficient Planarity Algorithm 。Robert Tarjan選定計算機科學領域作為他的主要研究方向,是因為他認為計算機科學是實踐數學理論的方式,有現實價值。
成就
Robert Tarjan設計了求解的套用領域的許多問題的廣泛有效的算法和數據結構。 他已發表了超過228篇理論文章(包括雜誌,一些書中的一些章節文章等)。Robert Tarjan以在數據結構和圖論上的開創性工作而聞名。 他的一些著名的算法包括 Tarjan最近共同祖先離線算法 ,Tarjan的強連通分量算法 以及Link-Cut-Trees算法等。其中Hopcroft-Tarjan平面嵌入算法是第一個線性時間平面算法。
Tarjan也開創了重要的數據結構如:斐波納契堆和splay樹(splay發明者還有Daniel Sleator)。另一項重大貢獻是分析了並查集。他是第一個證明了計算 反阿克曼函式的樂觀時間複雜度的科學家。
獎項
Tarjan與約翰霍普克羅夫特共同於1986年獲得圖靈獎。
Tarjan還於1994年當選為ACM院士。
Tarjan其他獎項包括:
奈望林納獎信息科學(1983第一個獲獎者)
國家科學院的研究倡議獎 (1984)
巴黎Kanellakis獎-理論與實踐( ACM1999)
帕斯卡獎章數學與計算機科學( 歐洲科學院2004)
加州理工學院傑出校友獎( 美國加州技術研究所2010)
算法介紹
LCA(Tarjan)
分類,使每個結點都落到某個類中,到時候只要執行集合查詢,就可以知道結點的LCA了。
對於一個結點u.類別有:
以u為根的子樹、除類一以外的以f(u)為根的子樹、除前兩類以外的以f(f(u))為根的子樹、除前三類以外的以f(f(f(u)))為根的子樹……
類一的LCA為u,類二為f(u),類三為f(f(u)),類四為f(f(f(u)))。這樣的分類看起來好像並不困難。
但關鍵是查詢是二維的,並沒有一個確定的u。接下來就是這個算法的巧妙之處了。
利用遞歸的LCA過程。
假設lca(u)執行完畢,則以u為根的子樹已經全部並為了一個集合。而一個lca的內部實際上做了的事就是對其子結點,依此調用lca.
設v1,v2,v3....vn為u的後繼結點且訪問順序為v1,v2,v3...vn
當v1(第一個子結點)被lca,正在處理v2的時候,以v1為根的子樹+u同在一個集合里,f(u)+編號比u小的u的兄弟的子樹 同在一個集合里,f(f(u)) + 編號比f(u)小的 f(u)的兄弟 的子樹 同在一個集合里……
而這些集合,對於v2的LCA都是不同的。因此只要查詢x在哪一個集合里,就能知道LCA(v2,x)
還有一種可能,x不在任何集合里。當他是v2的兒子,v3,v4等子樹或編號比u大的u的兄弟的子樹(等等)時,就會發生這種情況。即還沒有被處理。還沒有處理過的怎么辦?把一個查詢(x1,x2)往查詢列表里添加兩次,一次添加到x1的回答列表里,一次添加到x2的回答列表里,如果在做x1的時候發現 x2已經被處理了,那就接受這個詢問,未被處理就忽略。(兩次中必定只有一次詢問被接受).
複雜度為O(n+Qusetion times)Qusetion times為詢問次數
若需更加詳細,還可到“tarjan算法”處看看
實現用並查集
偽代碼如下:
//parent為並查集,FIND為並查集的查找操作
//QUERY為詢問結點對集合
//TREE為基圖有根樹
Tarjan(u)
visit[u] = true
for each (u, v) in QUERY
if visit[v]
ans(u, v) = FIND(v)
for each (u, v) in TREE
if !visit[v]
Tarjan(v)
parent[v] = u
cpp代碼:
強連通分量
首先我們把強連通分量看做一個齒輪或環(他會轉啊),不考慮其他的限制則可認為分量結點可以互換(就是轉一下)不會影響分量中包含的結點(理解tarjan時中的low值有幫助)
如圖(分量為S):
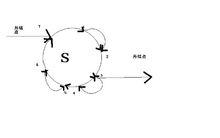 圖1
圖1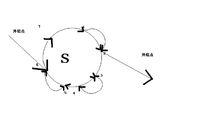 圖2
圖2Tarjan算法是基於對圖深度優先搜尋的算法,每個強連通分量為搜尋樹中的一棵子樹。搜尋時,把當前搜尋樹中未處理的節點加入一個堆疊,回溯時可以判斷棧頂到棧中的節點是否為一個強連通分量。
定義DFN(u)為節點u搜尋的次序編號(時間戳),Low(u)為u或u的子樹能夠追溯到的最早的棧中節點的次序號。由定義可以得出,
Low(u)=Min
{ DFN(u), Low(v),(u,v)為樹枝邊,u為v的父節點 DFN(v),(u,v)為指向棧中節點的後向邊(非橫叉邊)} 當DFN(u)=Low(u)時,以u為根的搜尋子樹上所有節點是一個強連通分量。
偽代碼:tarjan(u){
DFN[u]=Low[u]=++Index // 為節點u設定次序編號和Low初值
Stack.push(u) // 將節點u壓入棧中
for each (u, v) in E // 枚舉每一條邊
if (v is not visted) // 如果節點v未被訪問過
tarjan(v) // 繼續向下找
Low[u] = min(Low[u], Low[v])
else if (v in S) // 如果節點v還在棧內
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果節點u是強連通分量的根
repeat
v = S.pop // 將v退棧,為該強連通分量中一個頂點
print v
until (u== v)}
cpp:
pascal:

