Wallis公式

Wallis公式是關於圓周率的無窮乘積的公式，但Wallis公式中只有乘除運算，連開方都不需要，形式上十分簡單。雖然Wallis公式對π的近似計算沒有直接影響，但是在導出Stirling公式中起到了重要作用。

基本信息

• 中文名：華里士公式
• 英文名：Wallis Formula

• 提出時間：1655
• 套用學科：數學
• 適用領域範圍：數學，物理
• 提出者：wallis

公式內容

Wallis公式是關於圓周率的無窮乘積的公式，公式內容如下：

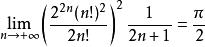Wallis公式

其中

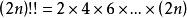Wallis公式

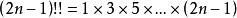Wallis公式

，

開方後還可以寫成：

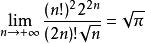Wallis公式

公式證明

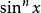Wallis公式

Wallis公式

對這一公式的證明採用對 在 的積分完成：

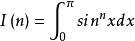Wallis公式

令

用分部積分法

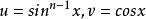Wallis公式

令

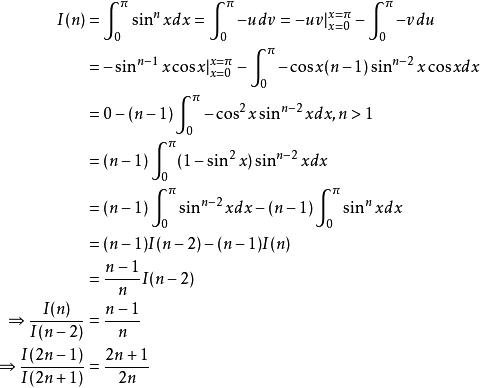Wallis公式

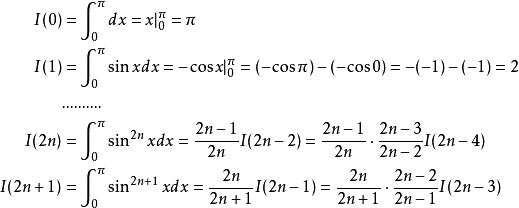Wallis公式

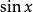Wallis公式

由 的單調性推知

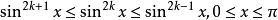Wallis公式

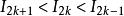Wallis公式

即為

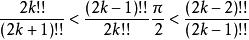Wallis公式

變形後得到

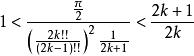Wallis公式

由求極限的夾逼準則，得到

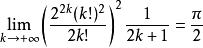Wallis公式

即為Wallis公式。

公式的變形

Wallis公式還有一些變形：

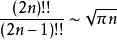Wallis公式

①

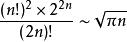Wallis公式

②

從①式可以看出Wallis公式的實質就是刻畫了雙階乘(2n)!!與(2n-1)!!之比的漸近性態。