雙階乘的定義
當n是自然數時,表示不超過n且與n有相同奇偶性的所有正整數的乘積。如:
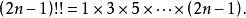 雙階乘
雙階乘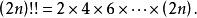 雙階乘
雙階乘示例:
3!!=1×3=3
5!!=1×3×5=15
6!!=2×4×6=48
8!!=2× 4×6×8=384
另0!!=1!!=1
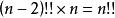 雙階乘
雙階乘當n是負奇數時,根據遞推公式,可知n!!的絕對值等於絕對值小於它的絕對值的所有負奇數的絕對值積的倒數,且正負交替出現。如:
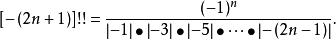 雙階乘
雙階乘示例:
(-5)!!=1/(|-1| × |-3|)=1/3
(-7)!!=-1/(|-1| × |-3| × |-5|)=-1/15
(-9)!!=1/(|-1| × |-3| × |-5| × |-7|)=1/105
另(-1)!!=1
當n是負偶數時,由遞推公式知(-2)!!=0!!/0無意義,故當n是負偶數時,n!!不存在。
恆等式
對於正整數n,有(2n-1)!!·(2n)!!=[1×3×…×(2n-1)]·[2×4×…×(2n)]=(2n)!
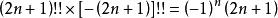 雙階乘
雙階乘對於任意整數n,有
定義域的擴展
當把雙階乘的定義域擴展到實數域的時候,雙階乘的值改變了,如 :
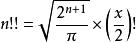 雙階乘
雙階乘其中(x/2)!的定義參見伽瑪函式。
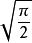 雙階乘
雙階乘在此定義下,奇數的雙階乘值沒有改變,而偶數的雙階乘值在原定義上除以。
注意到在此定義下第二條恆等式依然成立。
關於積分的恆等式
對於第二種定義下的雙階乘,滿足恆等式 :
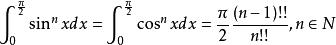 雙階乘
雙階乘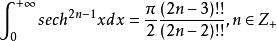 雙階乘
雙階乘以及
部分雙階乘的值
| n | 第一種定義下的n!! | 第二種定義下的n!! |
| 7 | 105 | 105 |
| 8 | 384 | 306.387671348300 |
| 9 | 945 | 945 |
| 10 | 3840 | 3063.876713483003 |
| 11 | 10395 | 10395 |
| 12 | 46080 | 36766.520561796031 |
| 13 | 135135 | 135135 |
| 14 | 645120 | 514731.287865144433 |
| 15 | 2027025 | 2027025 |

