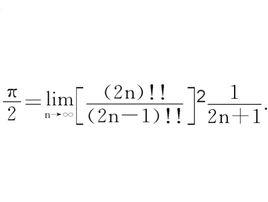基本介紹
形如
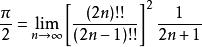 沃利斯公式
沃利斯公式的公式稱為 沃利斯公式。
它可以通過
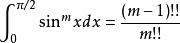 沃利斯公式
沃利斯公式(m為奇數整數)和
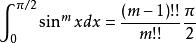 沃利斯公式
沃利斯公式(m為偶數整數)
得到,這個公式最早由沃利斯(J.Wallis)得到,並於1655年發表。他原來的結果是
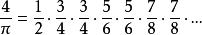 沃利斯公式
沃利斯公式這不僅是數學史上較早的無窮乘積的例子,也是第一個將π表為容易計算的有理數列的極限的公式,但對π的計算,現在已有快速的方法 。
相關介紹
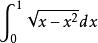 沃利斯公式
沃利斯公式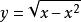 沃利斯公式
沃利斯公式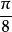 沃利斯公式
沃利斯公式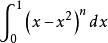 沃利斯公式
沃利斯公式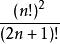 沃利斯公式
沃利斯公式沃利斯無疑是牛頓之前最重要的英國數學家,他在無窮小分析領域做出他最重要的貢獻。其中一項貢獻是,在計算的值時,他領先於歐拉論述伽馬函式(或階乘函式)的某些作品。從卡瓦列里、費馬及其他人的作品中,沃利斯得知,這個積分代表了半圓的面積,因此,這個面積是。但是,如何能夠用無窮小的方法,通過直接求這個積分的值來得到答案呢?沃利斯回答不了這個問題,但他的歸納法和插值法產生了一個十分有趣的結果。在針對n的幾個正整數值求出的值之後,沃利斯通過不完全歸納法得出了這樣一個結論:這個積分的值是。假設這個公式也適用於n的分數值,沃利斯得出結論:
 沃利斯公式
沃利斯公式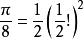 沃利斯公式
沃利斯公式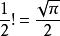 沃利斯公式
沃利斯公式式中,或者。這是歐拉的貝塔函式的一個特例,即:
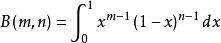 沃利斯公式
沃利斯公式式中,
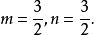 沃利斯公式
沃利斯公式在那些批評沃利斯的幾何算術化的人當中,托馬斯·霍布斯(1588~1679)是最重要的一位,他極力反對“把代數套用於幾何的整個群體”,並把《無窮算術》稱為“符號的瘡痂”。然而,霍布斯的數學自負超過他的數學能力。他堅持認為,已經解決了化圓為方及其他古代幾何問題。沃利斯完全有資格不理睬霍布斯,繼續做出更多的發現。他最有名的成果當中包括下面這個無窮乘積:
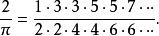 沃利斯公式
沃利斯公式這個表達式很容易得到,只要利用下面這個現代定理:
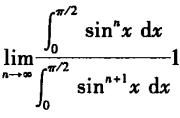 沃利斯公式
沃利斯公式再加上下面這兩個公式:
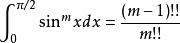 沃利斯公式
沃利斯公式(m為奇數整數)和
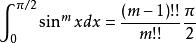 沃利斯公式
沃利斯公式(m為偶數整數)
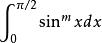 沃利斯公式
沃利斯公式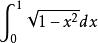 沃利斯公式
沃利斯公式(符號m!!代表乘積m(m-2) (m-4) ... ,它依據m是奇數還是偶數結束於1或2。)因此,上述求的公式被稱作 沃利斯公式。然而,沃利斯用來實現他那個求2/π的無窮乘積的方法,實際上還是基於他的歸納和插值原理,這一次是套用於,這個積分他不能直接求出,因為缺少二項式定理 。