基本介紹
設
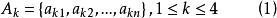T矩陣是長為n的(0,±1)-序列，若
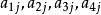T矩陣(i)對1≤j≤n，恰有一個為±1,其餘3個均為0，
(ii)對1≤j≤n-1,恆有
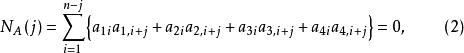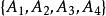T矩陣
T矩陣則稱是一組不相交T-序列。簡稱 T-序列(T-sequence)。
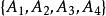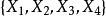T矩陣
T矩陣對上述T-序列，設1≤i≤4，令X表示以A為第一行而生成的n階循環矩陣，則稱為一組n階不相交循環T-矩陣，簡稱 循環T-矩陣。
用T-矩陣構造Baumert-Hall陣列
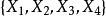T矩陣引理1設為n階循環T-矩陣。則
(i)1≤i,j≤4,i≠j,則X與X不相交,即
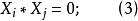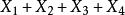T矩陣
T矩陣(ii)是一個(1,-1)-矩陣；
(iii)
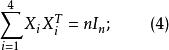T矩陣(iv)對1≤i≤4,X的各行和都相等,設X的行和為n,則
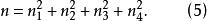T矩陣下述定理給出構作Baumert-Hall陣列的一個強有力方法。
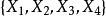T矩陣定理1(Cooper，J.Wallis) 設為n階循環T-矩陣，a，b，c，d為交換變元，令
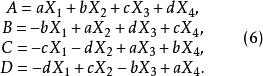T矩陣再設R為下述n×n矩陣：
式（7）將式(6)與式(7)代入下述Goethal-Seidel陣列
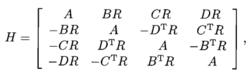式（8）則得到一個OD(4n；n，n，n，n)。
在上述定理中，若取a=b=c=d=1，則得到一個4n階H-陣，於是得到下述結果。
定理2若存在一組長為n的T-序列。則存在4n階H-陣。
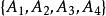T矩陣由定理1與定理2可見T-序列在構作Baumert-Hall陣列和Hadamard矩陣時所起的重要作用。一般來說，尋求長為n的T-序列並不容易。由引理1之(iv)可知。設是一組長為n的T-序列，又設A中所有元素的和為n，1≤i≤4，則必有
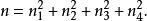T矩陣這一觀察有助於尋找T-序列。由Lagrange四平方和定理，任一正整數n都能表為4個非負整數的平方和，但是否對每一個正整數n都存在長為n的T-序列?這是一個尚未解決的問題，從對構作Hadamard矩陣的套用而言，我們主要關心n為奇數時T-序列的存在性。
猜想1 設n≥1為奇數，則存在長為n的T-序列。
若上述猜想成立，則作為其推論，Hadamard猜想也就得到證明。
定理3若4n≤200，則4n階H-陣存在。
