基礎知識
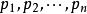 機率矩陣
機率矩陣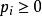 機率矩陣
機率矩陣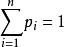 機率矩陣
機率矩陣機率向量:任意一個行向量P=( )如果滿足: (1<i<n)及 ,則向量P稱為機率向量。
 機率矩陣
機率矩陣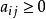 機率矩陣
機率矩陣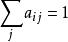 機率矩陣
機率矩陣機率矩陣:一個n階方陣A=( )如果滿足: , ,則稱方陣為機率矩陣。
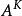 機率矩陣
機率矩陣正規機率矩陣:若A為n階機率矩陣,而且存在一個正整數K,使矩陣 沒有零元素,則稱A為正規機率矩陣。
不變向量:設u為n維非零行向量,A是n階方陣,如果u A = u,則稱u為是n階方陣A的不變向量。
固有向量:設X為機率向量,P為正規機率矩陣,如有XP=X存在,則稱X為P的固有向量。
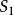 機率矩陣
機率矩陣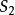 機率矩陣
機率矩陣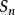 機率矩陣
機率矩陣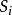 機率矩陣
機率矩陣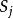 機率矩陣
機率矩陣 機率矩陣
機率矩陣轉移機率:考慮一個具有n個結果(狀態) , ,…, 的系統,如果系統由狀態 變化到 ,就稱為系統的狀態轉移,其機率 就稱為狀態轉移機率,簡稱轉移機率。
 機率矩陣
機率矩陣 機率矩陣
機率矩陣狀態轉移矩陣:由狀態轉移機率 (i=1,2,…n)(j=1,2,…n)構成的矩陣P=( )叫狀態轉移矩陣。
馬爾可夫過程:如果一個系統在狀態轉移過程中下一步處於什麼狀態與且僅與現在的狀態有關,而與過去的狀態無關,這種過程稱為馬爾可夫過程。若馬爾可夫鏈的狀態轉移機率矩陣為正規機率矩陣,當轉移步數K逐漸增大,轉移機率矩陣將趨向某一穩態機率矩陣。
相關定理
1.若A、B都為n階機率矩陣,則A*B也是n階機率矩陣。由於矩陣乘法不滿足交換律,當然機率矩陣乘法也不滿足交換律。
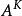 機率矩陣
機率矩陣2.若A為n階機率矩陣,K為任意正整數,則 也是n階機率矩陣。
3.機率矩陣對加減運算不是封閉的。
4.機率矩陣A的行列式| A|,其值的絕對值0≤ | A| ≤ 1。
5. n階機率矩陣的逆矩陣不一定是機率矩陣,故不能進行求逆運算。
 機率矩陣
機率矩陣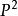 機率矩陣
機率矩陣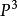 機率矩陣
機率矩陣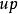 機率矩陣
機率矩陣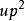 機率矩陣
機率矩陣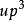 機率矩陣
機率矩陣設P是正規的機率矩陣,則
1.P有且僅有一個不變機率向量t,而且t的所有元素都為正數。
2.矩陣序列
3.設u為任意一個機率向量,則向量序列,,….趨近於不變機率向量t。
相關計算
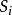 機率矩陣
機率矩陣 機率矩陣
機率矩陣 機率矩陣
機率矩陣 機率矩陣
機率矩陣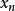 機率矩陣
機率矩陣如果一個馬爾可夫過程是正規的,即它的狀態轉移矩陣P是正規機率矩陣,那么系統一定能通過狀態轉移達到某一個穩定狀態。設在穩定狀態下,系統處於狀態 的機率為 (i=1,2,…n),記X=( , ..., )。
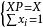 機率矩陣
機率矩陣通過求解聯立方程組 ,可求出系統處於穩定狀態的不變向量X。
套用實例
例1.已知在某地區銷售同類型產品的有A,B,C三個公司,經過一年營業後進行調查,發現:A公司的200名顧客中有160名繼續訂貨,有20名轉向B公司訂貨,20名轉向C公司訂貨。B公司的500名顧客中有450名繼續訂貨,有35名轉向A公司訂貨,15名轉向C公司訂貨。C公司的300名顧客中有255名繼續訂貨,有25名轉向A公司訂貨,20名轉向B公司訂貨。
如果三個公司在這個地區的初始占有率為A=22%,B=49%,C=29% , 且它們都不改變營業狀態和規模,問:
(1)明年和後年,三個公司在這個地區市場占有率為如何?
(2)穩定狀態下,三個公司的市場占有率?
解:
(1)根據題意,狀態轉移矩陣為:
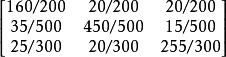 機率矩陣
機率矩陣狀態轉移矩陣化簡為:
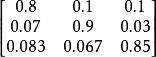 機率矩陣
機率矩陣今年的市場占有率u=(0.22,0.49,0.29);
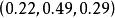 機率矩陣
機率矩陣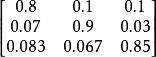 機率矩陣
機率矩陣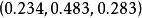 機率矩陣
機率矩陣明年的市場占有率up= = ;
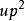 機率矩陣
機率矩陣後年的市場占有率 =(0.245,0.477,0.278)。
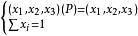 機率矩陣
機率矩陣(2)穩定狀態下,市場占有率將是: ;
 機率矩陣
機率矩陣 機率矩陣
機率矩陣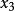 機率矩陣
機率矩陣得: = 0.273; = 0.454; = 0.273。所以,穩定狀態下,三個公司的市場占有率分別為0.273、0.454、0.273。

