定義
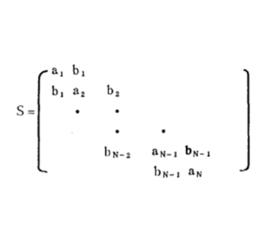
形如
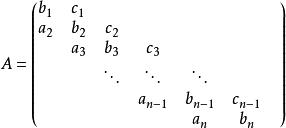 三對角矩陣
三對角矩陣的n×n矩陣A稱為三對角矩陣,其中第(i,j)個元素在j>i+1和j<i-1時為零。
三對角矩陣的建立
分析矩陣特點
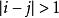 三對角矩陣
三對角矩陣三對角矩陣M是一個對角矩陣,若且唯若 時,有M(i,j)=0。在一個nxn的三對角矩陣T中,非0元素排列在如下的三條對角線上:
(1)主對角線即i=j;
(2)主對角線之下的對角線(稱低對角線)即i=j+1;
(3)主對角線之上的對角線(稱高對角線)即i=j-1。
這三條對角線上的元素總數為3n-2,故可以使用一個擁有3n-2個位置的一維數組來描述T,因為僅需要存儲三條對角線上的元素。
矩陣實例
考察如下所示的4×4三對角矩陣:
 三對角矩陣
三對角矩陣三對角矩陣上共有10個元素,如果把這些元素逐行映射到t中,則有t[0:9]=[2,1,3,1,3,5,2,7,9,0];如果逐列映射到t上,則有t[0:9]=[2,3,1,1,5,3,2,9,7,0];如果按照對角線的次序(從最下面的對角線開始)進行映射,則有t[0:9]=[3,5,9,2,1,2,0,1,3,7]。
建立該三對角矩陣的程式
利用Store函式把傳入的x值存儲在相應的三對角矩陣中,並通過switch語句判斷其所在位置。具體程式如下:
確定三對角矩陣的特徵值
QR法
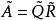 三對角矩陣
三對角矩陣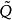 三對角矩陣
三對角矩陣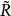 三對角矩陣
三對角矩陣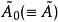 三對角矩陣
三對角矩陣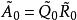 三對角矩陣
三對角矩陣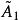 三對角矩陣
三對角矩陣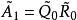 三對角矩陣
三對角矩陣QR法對於三對角矩陣來說是很好的,在這個方法中,矩陣被分解成以下形式: ,其中 是正交矩陣, 是上三角矩陣。產生如下的矩陣序列:將 化成乘積形式 ,則 定義為 。
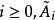 三對角矩陣
三對角矩陣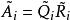 三對角矩陣
三對角矩陣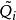 三對角矩陣
三對角矩陣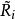 三對角矩陣
三對角矩陣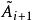 三對角矩陣
三對角矩陣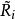 三對角矩陣
三對角矩陣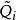 三對角矩陣
三對角矩陣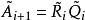 三對角矩陣
三對角矩陣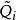 三對角矩陣
三對角矩陣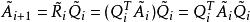 三對角矩陣
三對角矩陣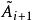 三對角矩陣
三對角矩陣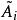 三對角矩陣
三對角矩陣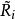 三對角矩陣
三對角矩陣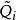 三對角矩陣
三對角矩陣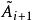 三對角矩陣
三對角矩陣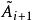 三對角矩陣
三對角矩陣一般來說,對於 化成 ,其中 是正交矩陣, 是上三角矩陣,則 被定義為 和 以相反次序乘積式,即 。因為 是正交矩陣, 。 是對稱的,與 有相同的特徵值。我們定義和成這樣的形式:是三對角矩陣,最終趨於變為對角陣,其對角線上的元素給出原矩陣的特徵值。
特徵多項式法
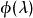 三對角矩陣
三對角矩陣特徵多項式法可以像特徵多項式的根一樣確定特徵值。有一種有效的方法來構造三對角矩陣的特徵多項式。使用符號法可以求特徵值的歸類,從而形成一個Sturmian序列。然後用對分法或試位法來求精確的特徵值。由Householder變換得到的對稱三對角矩陣的特徵多項式為:
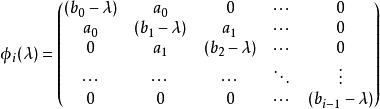 三對角矩陣
三對角矩陣其中,i=1,2,...,n,有:
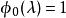 三對角矩陣
三對角矩陣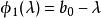 三對角矩陣
三對角矩陣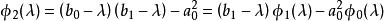 三對角矩陣
三對角矩陣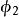 三對角矩陣
三對角矩陣從向前的Sturm序列可以表示為:
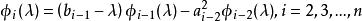 三對角矩陣
三對角矩陣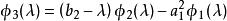 三對角矩陣
三對角矩陣因此,有
實例
求下述三對角矩陣的特徵多項式:
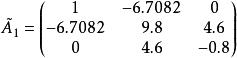 三對角矩陣
三對角矩陣解:把該矩陣與特徵多項式的一般形式作比較,則有
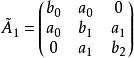 三對角矩陣
三對角矩陣比較這兩個矩陣,得到
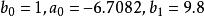 三對角矩陣
三對角矩陣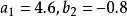 三對角矩陣
三對角矩陣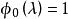 三對角矩陣
三對角矩陣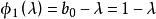 三對角矩陣
三對角矩陣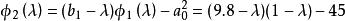 三對角矩陣
三對角矩陣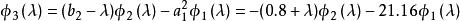 三對角矩陣
三對角矩陣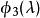 三對角矩陣
三對角矩陣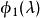 三對角矩陣
三對角矩陣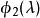 三對角矩陣
三對角矩陣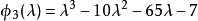 三對角矩陣
三對角矩陣在的表達式中代入和的值並化簡,得到:。