基本定義
只有當矩陣 A的列數與矩陣 B的行數相等時 A× B才有意義。一個 m× n的矩陣 a(m, n)左乘一個 n× p的矩陣 b(n, p),會得到一個 m× p的矩陣 c(m, p),滿足
矩陣乘法滿足結合律,但不滿足交換律
一般的矩乘要結合快速冪才有效果。(基本上所有矩陣乘法都要用到快速冪的)
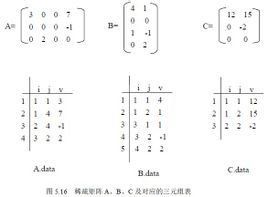
在計算機中,一個矩陣說穿了就是一個二維數組。一個n行m列的矩陣可以乘以一個m行p列的矩陣,得到的結果是一個n行p列的矩陣,其中的第i行第j列位置上的數等於前一個矩陣第i行上的m個數與後一個矩陣第j列上的m個數對應相乘後所有m個乘積的和。比如,下面的算式表示一個2行2列的矩陣乘以2行3列的矩陣,其結果是一個2行3列的矩陣。其中,結果的那個4等於2*2+0*1:
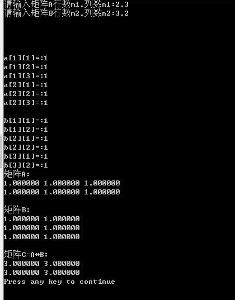
矩陣乘法的c語言程式:
#include
float main()
{
float a,b,c;//定義三個數組,分別存儲矩陣A,B,C
int m1,n1,m2,n2,i1,j1,i2,j2,i3,j3,i4,j4,k;
float s={0};//賦值使數組s元素初值全部為零
printf("請輸入矩陣A行數m1,列數n1:");//輸入矩陣A行數,列數
scanf("%d,%d",&m1,&n1);
printf("請輸入矩陣B行數m2,列數n2:");//輸入矩陣B行數,列數
scanf("%d,%d",&m2,&n2);
printf("\n\n");//如果不可以相乘,下面將出現判斷,在此換行,便於觀看
if(n1!=m2)
printf("不可以相乘!!!");//判斷是否可以相乘
printf("\n\n");
if((m1>100)||(n1>100))
printf("數目過多!!!");//控制矩陣A元素數量在數組容納範圍內
else
{
for(i1=1;i1<=m1;i1++)
{
for(j1=1;j1<=n1;j1++)
{
printf("a[%d][%d]=:",i1,j1);
scanf("%f",&a[i1][j1]);//輸入矩陣A元素
}
}
}
printf("\n");//分隔開A,B的元素輸入,便於觀看
if((m2>100)||(n2>100))
printf("數目過多!!!");
else
{
for(i2=1;i2<=m2;i2++)
{
for(j2=1;j2<=n2;j2++)
{
printf("b[%d][%d]=:",i2,j2);
scanf("%f",&b[i2][j2]);//輸入矩陣B元素
}
}
}
printf("矩陣A:\n");//輸出矩陣A,便於觀看,檢驗
for(i3=1;i3<=m1;i3++)
{
for(j3=1;j3<=n1;j3++)
{
printf("%f ",a[i3][j3]);
if(j3==n1)
printf("\n");
}
}
printf("\n");//與矩陣B的輸出結果隔開,便於觀看
printf("矩陣B:\n");//輸出矩陣A,便於觀看,檢驗
for(i4=1;i4<=m2;i4++)
{
for(j4=1;j4<=n2;j4++)
{
printf("%f ",b[i4][j4]);
if(j4==n2)
printf("\n");
}
}
printf("\n");
printf("矩陣C=A*B:\n");
for(i4=1;i4<=m1;i4++)
{
for(j4=1;j4<=n2;j4++)
{
for(k=1;k<=n1;k++)
{
s[i4][j4]=s[i4][j4]+a[i4][k]*b[k][j4];//定義矩陣乘法,相乘時,有一個指標是一樣的,都用k
}
c[i4][j4]=s[i4][j4];//定義矩陣乘法
printf("%f ",c[i4][j4]);
if(j4==n2)
printf("\n");//控制在列指標到達N時換行
}
}
return 0;
}
 圖片展示
圖片展示程式運行結果示例: 一般矩乘的代碼:function mul( a , b : Tmatrix ) : Tmatrix;
var
i,j,k : longint;
c : Tmatrix;
begin
fillchar( c , sizeof( c ) , 0 );
for k:=0 to n do
for i:=0 to m do
for j:=0 to p do
begin
inc( c[ i , j ] , a[ i , k ]*b[ k , j ] );
if c[ i , j ] > ra then c[ i , j ]:=c[ i , j ] mod ra;
end;
mul:=c;
end;
這裡我們不介紹其它有關矩陣的知識,只介紹矩陣乘法和相關性質。
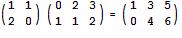 矩陣乘法
矩陣乘法不要以為數學中的矩陣也是黑色螢幕上不斷變化的綠色字元。在數學中,一個矩陣說穿了就是一個二維數組。一個n行m列的矩陣可以乘以一個m行p列的矩陣,得到的結果是一個n行p列的矩陣,其中的第i行第j列位置上的數等於前一個矩陣第i行上的m個數與後一個矩陣第j列上的m個數對應相乘後所有m個乘積的和。比如,下面的算式表示一個2行2列的矩陣乘以2行3列的矩陣,其結果是一個2行3列的矩陣。其中,結果的那個4等於2*2+0*1: 右面的算式則是一個1 x 3的矩陣乘以3 x 2的矩陣,得到一個1 x 2的矩陣:
矩陣乘法的兩個重要性質: 一,矩陣乘法不滿足交換律;二,矩陣乘法滿足結合律。為什麼矩陣乘法不滿足交換律呢?因為交換後兩個矩陣有可能不能相乘。為什麼它又滿足結合律呢?假設你有三個矩陣A、B、C,那么(AB)C和A(BC)的結果的第i行第j列上的數都等於所有A(ik)*B(kl)*C(lj)的和(枚舉所有的k和l)。
基本性質
1.結合性 ( AB) C= A( BC).
2.對加法的分配性 ( A+ B) C= AC+ BC, C( A+ B)= CA+ CB .
3.對數乘的結合性 k( AB)=( kA) B = A( kB).
4.關於轉置 (AB)'=B'A'.
經典題目
給定n個點,m個操作,構造O(m+n)的算法輸出m個操作後各點的位置。操作有平移、縮放、翻轉和鏇轉
這裡的操作是對所有點同時進行的。其中翻轉是以坐標軸為對稱軸進行翻轉(兩種情況),鏇轉則以原點為中心。如果對每個點分別進行模擬,那么m個操作總共耗時O(mn)。利用矩陣乘法可以在O(m)的時間裡把所有操作合併為一個矩陣,然後每個點與該矩陣相乘即可直接得出最終該點的位置,總共耗時O(m+n)。假設初始時某個點的坐標為x和y,下面5個矩陣可以分別對其進行平移、鏇轉、翻轉和鏇轉操作。預先把所有m個操作所對應的矩陣全部乘起來,再乘以(x,y,1),即可一步得出最終點的位置。
給定矩陣A,請快速計算出A^n(n個A相乘)的結果,輸出的每個數都modp。
由於矩陣乘法具有結合律,因此A^4=A*A*A*A=(A*A)*(A*A)=A^2*A^2。我們可以得到這樣的結論:當n為偶數時,A^n=A^(n/2)*A^(n/2);當n為奇數時,A^n=A^(n/2)*A^(n/2)*A(其中n/2取整)。這就告訴我們,計算A^n也可以使用二分快速求冪的方法。例如,為了算出A^25的值,我們只需要遞歸地計算出A^12、A^6、A^3的值即可。根據這裡的一些結果,我們可以在計算過程中不斷取模,避免高精度運算。
POJ3233題目大意:給定矩陣A,求A+A^2+A^3+...+A^k的結果(兩個矩陣相加就是對應位置分別相加)。輸出的數據modm。k<=10^9。
這道題兩次二分,相當經典。首先我們知道,A^i可以二分求出。然後我們需要對整個題目的數據規模k進行二分。比如,當k=6時,有:
A+A^2+A^3+A^4+A^5+A^6=(A+A^2+A^3)+A^3*(A+A^2+A^3)
套用這個式子後,規模k減小了一半。我們二分求出A^3後再遞歸地計算A+A^2+A^3,即可得到原問題的答案。
VOJ1049題目大意:順次給出m個置換,反覆使用這m個置換對初始序列進行操作,問k次置換後的序列。m<=10,k<2^31。
首先將這m個置換“合併”起來(算出這m個置換的乘積),然後接下來我們需要執行這個置換k/m次(取整,若有餘數則剩下幾步模擬即可)。注意任意一個置換都可以表示成矩陣的形式。例如,將1234置換為3124,相當於下面的矩陣乘法:
置換k/m次就相當於在前面乘以k/m個這樣的矩陣。我們可以二分計算出該矩陣的k/m次方,再乘以初始序列即可。做出來了別忙著高興,得意之時就是你滅亡之日,別忘了最後可能還有幾個置換需要模擬。
《算法藝術與信息學競賽》207頁(2.1代數方法和模型,[例題5]細菌,版次不同可能頁碼有偏差)
大家自己去看看吧,書上講得很詳細。解題方法和上一題類似,都是用矩陣來表示操作,然後二分求最終狀態。
給定n和p,求第n個Fibonacci數modp的值,n不超過2^31
根據前面的一些思路,現在我們需要構造一個2x2的矩陣,使得它乘以(a,b)得到的結果是(b,a+b)。每多乘一次這個矩陣,這兩個數就會多疊代一次。那么,我們把這個2x2的矩陣自乘n次,再乘以(0,1)就可以得到第n個Fibonacci數了。不用多想,這個2x2的矩陣很容易構造出來:
VOJ1067我們可以用上面的方法二分求出任何一個線性遞推式的第n項,其對應矩陣的構造方法為:在右上角的(n-1)*(n-1)的小矩陣中的主對角線上填1,矩陣第n行填對應的係數,其它地方都填0。例如,我們可以用下面的矩陣乘法來二分計算f(n)=4f(n-1)-3f(n-2)+2f(n-4)的第k項:
利用矩陣乘法求解線性遞推關係的題目我能編出一卡車來。這裡給出的例題是係數全為1的情況。
給定一個有向圖,問從A點恰好走k步(允許重複經過邊)到達B點的方案數modp的值
把給定的圖轉為鄰接矩陣,即A(i,j)=1若且唯若存在一條邊i->j。令C=A*A,那么C(i,j)=ΣA(i,k)*A(k,j),實際上就等於從點i到點j恰好經過2條邊的路徑數(枚舉k為中轉點)。類似地,C*A的第i行第j列就表示從i到j經過3條邊的路徑數。同理,如果要求經過k步的路徑數,我們只需要二分求出A^k即可。
 矩陣乘法
矩陣乘法 矩陣乘法
矩陣乘法 矩陣乘法
矩陣乘法用1x2的多米諾骨牌填滿MxN的矩形有多少種方案,M<=5,N<2^31,輸出答案modp的結果
我們以M=3為例進行講解。假設我們把這個矩形橫著放在電腦螢幕上,從右往左一列一列地進行填充。其中前n-2列已經填滿了,第n-1列參差不齊。現在我們要做的事情是把第n-1列也填滿,將狀態轉移到第n列上去。由於第n-1列的狀態不一樣(有8種不同的狀態),因此我們需要分情況進行討論。在圖中,我把轉移前8種不同的狀態放在左邊,轉移後8種不同的狀態放在右邊,左邊的某種狀態可以轉移到右邊的某種狀態就在它們之間連一根線。注意為了保證方案不重複,狀態轉移時我們不允許在第n-1列豎著放一個多米諾骨牌(例如左邊第2種狀態不能轉移到右邊第4種狀態),否則這將與另一種轉移前的狀態重複。把這8種狀態的轉移關係畫成一個有向圖,那么問題就變成了這樣:從狀態111出發,恰好經過n步回到這個狀態有多少種方案。比如,n=2時有3種方案,111->011->111、111->110->111和111->000->111,這與用多米諾骨牌復蓋3x2矩形的方案一一對應。這樣這個題目就轉化為了我們前面的例題8。
後面我寫了一份此題的原始碼。你可以再次看到位運算的相關套用。
經典題目10POJ2778
題目大意是,檢測所有可能的n位DNA串有多少個DNA串中不含有指定的病毒片段。合法的DNA只能由ACTG四個字元構成。題目將給出10個以內的病毒片段,每個片段長度不超過10。數據規模n<=2000000000。
下面的講解中我們以ATC,AAA,GGC,CT這四個病毒片段為例,說明怎樣像上面的題一樣通過構圖將問題轉化為例題8。我們找出所有病毒片段的前綴,把n位DNA分為以下7類:以AT結尾、以AA結尾、以GG結尾、以?A結尾、以?G結尾、以?C結尾和以?結尾。其中問號表示“其它情況”,它可以是任一字母,只要這個字母不會讓它所在的串成為某個病毒的前綴。顯然,這些分類是全集的一個劃分(交集為空,並集為全集)。現在,假如我們已經知道了長度為n-1的各類DNA中符合要求的DNA個數,我們需要求出長度為n時各類DNA的個數。我們可以根據各類型間的轉移構造一個邊上帶權的有向圖。例如,從AT不能轉移到AA,從AT轉移到?有4種方法(後面加任一字母),從?A轉移到AA有1種方案(後面加個A),從?A轉移到?有2種方案(後面加G或C),從GG到?有2種方案(後面加C將構成病毒片段,不合法,只能加A和T)等等。這個圖的構造過程類似於用有限狀態自動機做串匹配。然後,我們就把這個圖轉化成矩陣,讓這個矩陣自乘n次即可。最後輸出的是從?狀態到所有其它狀態的路徑數總和。
乘法算法
傳統算法:
若依定義來計算A和B的乘積矩陣C,則每計算C的一個元素C[i][j],需要做n次乘法和n-1次加法。因此,算出矩陣C的個元素所需的計算時間為O(n3)
Strassen矩陣乘法:
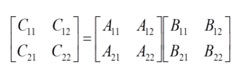 矩陣乘法
矩陣乘法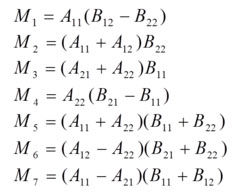 矩陣乘法
矩陣乘法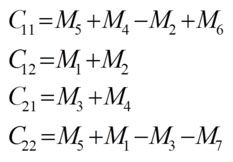 矩陣乘法
矩陣乘法T(n)=O(nlog7)=O(n2.81)時間複雜度有了較大改進!
目前最好的計算時間上界是O(n2.376)