定義
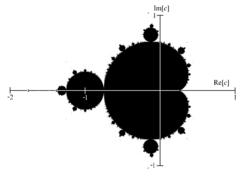
曼德布洛特集合(Mandelbrot set)是在複平面上組成分形的點的集合。Mandelbrot集合可以用復二次多項式f(z)=z^2+c來定義。
其中c是一個復參數。對於每一個c,從z=0開始對f(z)進行疊代
序列 (0, f(0), f(f(0)), f(f(f(0))), .......)的值或者延伸到無限大,或者只停留在有限半徑的圓盤內。
曼德布洛特集合就是使以上序列不延伸至無限大的所有c點的集合。
從數學上來講,曼德布洛特集合是一個複數的集合。一個給定的複數c或者屬於曼德布洛特集合M,或者不是。
圖例:如果c點屬於曼德布洛特集合M則為黑色,反之為白色
計算的方法
曼德布洛特集合一般用電腦程式計算。對於大多數的分形軟體,例如Ultra fractal,內部已經有了比較成熟的例子。下面的程式是一段偽代碼,表達了曼德布洛特集合的計算思路。
For Each z0 in Complex
repeats = 0
z=z0
Do
z=z^2+z0
repeate = repeats+1
Loop until abs(z)>bailout or repeats >= MaxRepeats
If repeats >= MaxRepeats Then
Draw z0,Black
Else
Draw z0,f(z,z0,Repeats) 'f返回顏色
End If
Next
