Mandelbrot集

repeats repeate iteration

簡介

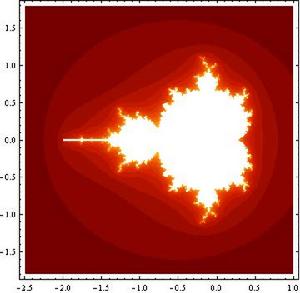Mandelbrot集的圖片

曼德布洛特集合（Mandelbrot set）是在複平面上組成分形的點的集合。Mandelbrot集合可以用復二次多項式f(z)=z^2+c來定義。
其中c是一個復參數。對於每一個c，從z=0開始對f(z)進行疊代
序列 (0, f(0), f(f(0)), f(f(f(0))), .......)的值或者延伸到無限大，或者只停留在有限半徑的圓盤內。
曼德布洛特集合就是使以上序列不延伸至無限大的所有c點的集合。
從數學上來講，曼德布洛特集合是一個複數的集合。一個給定的複數c或者屬於曼德布洛特集合M，或者不是。

計算的方法

曼德布洛特集合一般用電腦程式計算。對於大多數的分形軟體，例如Ultra fractal，內部已經有了比較成熟的例子。下面的程式是一段偽代碼，表達了曼德布洛特集合的計算思路。
For Each z0 in Complex
repeats = 0
z=z0
Do
z=z^2+z0
repeate = repeats+1
Loop until abs(z)>bailout or repeats >= MaxRepeats
If repeats >= MaxRepeats Then
Draw z0,Black
Else
Draw z0,f(z,z0,Repeats) 'f返回顏色
End If
Next

Mandelbrot 圖像C#原始碼

using System;
using System.Collections.Generic;
using System.Text;
// Mandelbrot Image
// Created by Rich on 2009-3-25
namespace Ch4Ex06
{
class Program
{
static void Main(string[] ARGs)
{
double realCoord, imagCoord;
double realTemp, imagTemp, realTemp2, arg;
int iterations;
for (imagCoord = 1.2; imagCoord >= -1.2; imagCoord -= 0.05)
{
for (realCoord = -0.6; realCoord <= 1.77; realCoord += 0.03)
{
iterations = 0;
realTemp = realCoord;
imagTemp = imagCoord;
arg = (realCoord * realCoord) + (imagCoord * imagCoord);
while ((arg < 4) && (iterations < 40))
{
realTemp2 = (realTemp * realTemp) - (imagTemp * imagTemp)
- realCoord;
imagTemp = (2 * realTemp * imagTemp) - imagCoord;
realTemp = realTemp2;
arg = (realTemp * realTemp) + (imagTemp * imagTemp);
iterations += 1;
}
switch (iterations % 4)
{
case 0:
Console.Write(".");
break;
case 1:
Console.Write("o");
break;
case 2:
Console.Write("0");
break;
case 3:
Console.Write("@");
break;
}
}
Console.Write("\n");
}
Console.ReadKey();
}
}
}

C++程式原始碼實現

#include <iostream>
using namespace std;
int main()
{
double realCoord, imagCoord;
double raalTemp, imagTemp, realTemp2, arg;
int iterations;
for (imagCoord = 1.2; imagCoord >= -1.2; imagCoord -= 0.05)
{
for(realCoord = -0.6; realCoord <=1.77;realCoord += 0.03)
{
iterations = 0;
raalTemp = realCoord;
imagTemp = imagCoord;
arg = (realCoord + realCoord) + (imagCoord * imagCoord);
while ((arg < 4) && (iterations < 40))
{
realTemp2 = (raalTemp * raalTemp) - (imagTemp * imagTemp)
-realCoord;
imagTemp = (2 * raalTemp * imagTemp) - imagCoord;
raalTemp = realTemp2;
arg = (raalTemp * raalTemp) + (imagTemp * imagTemp);
iterations += 1;
}
switch (iterations % 4)
{
case 0:
cout<<".";
break;
case 1:
cout<<"o";
break;
case 2:
cout<<"O";
break;
case 3:
cout<<"@";
break;
default:
break;
}
}
cout<<"\n";
cin.get();
}
system("pause");
return 0;
}
運行結果：

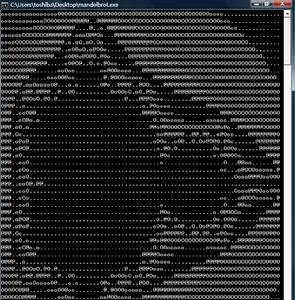C++程式實現Mandelbrot

C#程式原始碼實現

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace TestFor
{
class Program
{
static void Main(string&#91;&#93; args)
{
double realCoord, imagCoord;
double raalTemp, imagTemp, realTemp2, arg;
int iterations;
for (imagCoord = 1.2; imagCoord >= -1.2; imagCoord -= 0.05)
{
for(realCoord = -0.6; realCoord<=1.77;realCoord+=0.03)
{
iterations = 0;
raalTemp = realCoord;
imagTemp = imagCoord;
arg = (realCoord + realCoord) + (imagCoord * imagCoord);
while ((arg < 4) && (iterations < 40))
{
realTemp2 = (raalTemp * raalTemp) - (imagTemp * imagTemp)
- realCoord;
imagTemp = (2 * raalTemp * imagTemp) - imagCoord;
raalTemp = realTemp2;
arg = (raalTemp * raalTemp) + (imagTemp * imagTemp);
iterations += 1;
}
switch (iterations % 4)
{
case 0:
Console.Write(".");
break;
case 1:
Console.Write("o");
break;
case 2:
Console.Write("O");
break;
case 3:
Console.Write("@");
break;
default:
break;
}
}
Console.Write("\n");
}
Console.ReadKey();
}
}
}
運行結果：

Mandelbrot圖像的程式實現結果

Mathematica代碼實現

DensityPlot&#91;(n = 1; z = x + I y;
While&#91;n < 100 && Abs&#91;z&#93; < 100, z = z^2 + x + I y; n++&#93;; n), {x, -2, 1}, {y, -1.5, 1.5}, PlotPoints -> 80&#93;

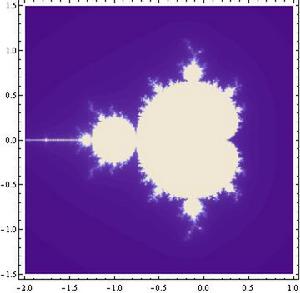用Mathematica做出的Mandelbrot集

MAPLE代碼實現

with(plots);
mm := proc (x, y)
local z, i;
z := x+I*y;
for i to 50 while abs(z) < 5. do z := z^2+x+I*y end do;
i
end proc;
listdensityplot(&#91;seq(&#91;seq(mm(x, y), x = -2 .. 1, 0.2e-1)&#93;, y = -1.5 .. 1.5, 0.2e-1)&#93;, smooth = true, axes = none)

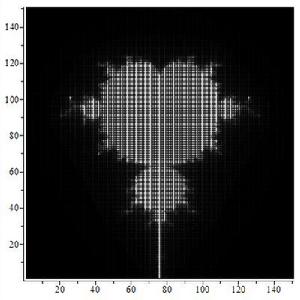用MAPLE做出的mandelbrot集。