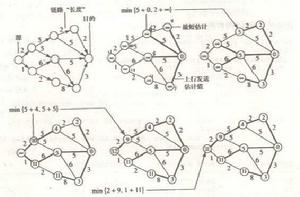
介紹
Dijkstra算法無法判斷含負權邊的圖的最短路。如果遇到負權,在沒有負權迴路(迴路的權值和為負,即便有負權的邊)存在時,也可以採用Bellman - Ford算法正確求出最短路徑。
Bellman-Ford算法能在更普遍的情況下(存在負權邊)解決單源點最短路徑問題。對於給定的帶權(有向或無向)圖 G=(V,E), 其源點為s,加權函式 w是 邊集 E 的映射。對圖G運行Bellman - Ford算法的結果是一個布爾值,表明圖中是否存在著一個從源點s可達的負權迴路。若不存在這樣的迴路,算法將給出從源點s到 圖G的任意頂點v的最短路徑d[v]。
適用條件
1.單源最短路徑(從源點s到其它所有頂點v);
2.有向圖&無向圖(無向圖可以看作(u,v),(v,u)同屬於邊集E的有向圖);
3.邊權可正可負(如有負權迴路輸出錯誤提示);
4.差分約束系統;
算法描述
1,.初始化:將除源點外的所有頂點的最短距離估計值 d[v] ——>+∞, d[s]——>0;
2.疊代求解:反覆對邊集E中的每條邊進行鬆弛操作,使得頂點集V中的每個頂點v的最短距離估計值逐步逼近其最短距離;(運行|v|-1次)
3.檢驗負權迴路:判斷邊集E中的每一條邊的兩個端點是否收斂。如果存在未收斂的頂點,則算法返回false,表明問題無解;否則算法返回true,並且從源點可達的頂點v的最短距離保存在 d[v]中。
描述性證明
首先指出,圖的任意一條最短路徑既不能包含負權迴路,也不會包含正權迴路,因此它最多包含|v|-1條邊。
其次,從源點s可達的所有頂點如果 存在最短路徑,則這些最短路徑構成一個以s為根的最短路徑樹。Bellman-Ford算法的疊代鬆弛操作,實際上就是按每個點實際的最短路徑[雖然我們還不知道,但它一定存在]的層次,逐層生成這棵最短路徑樹的過程。
注意,每一次遍歷,都可以從前一次遍歷的基礎上,找到此次遍歷的部分點的單源最短路徑。如:這是第i次遍歷,那么,通過數學歸納法,若前面單源最短路徑層次為1~(i-1)的點全部已經得到,而單源最短路徑層次為i的點,必定可由單源最短路徑層次為i-1的點集得到,從而在下一次遍歷中充當前一次的點集,如此往復疊代,[v]-1次後,若無負權迴路,則我們已經達到了所需的目的--得到每個點的單源最短路徑。[注意:這棵樹的每一次更新,可以將其中的某一個子樹接到另一個點下]
反之,可證,若存在負權迴路,第[v]次遍歷一定存在更新,因為負權迴路的環中,必定存在一個“斷點”,可用數學手段證明。
最後,我們在第[v]次更新中若沒有新的鬆弛,則輸出結果,若依然存在鬆弛,則輸出‘CAN'T'表示無解。同時,我們還可以通過“斷點”找到負權迴路。
偽代碼
時間複雜度
算法時間複雜度O(VE)。因為算法簡單,適用範圍又廣,雖然複雜度稍高,仍不失為一個很實用的算法。
參考代碼
PASCAL
{單源最短路徑的Bellman-ford算法
執行v-1次,每次對每條邊進行鬆弛操作
如有負權迴路則輸出"Error!!"}
Matlab
C++
引申內容
SPFA算法
SPFA(Shortest Path Faster Algorithm)是Bellman-Ford算法的一種佇列最佳化,減少了不必要的冗餘計算。
算法流程
算法大致流程是用一個佇列來進行維護。 初始時將源加入佇列。 每次從佇列中取出一個元素,並對所有與他相鄰的點進行鬆弛,若某個相鄰的點鬆弛成功,則將其入隊。 直到佇列為空時算法結束。
算法代碼
算法的最佳化
分析 Bellman-Ford算法,不難看出,外層循環(疊代次數)|v|-1實際上取得是上限。由上面對算法正確性的證明可知,需要的疊代遍數等於最短路徑樹的高度。如果不存在負權迴路,平均情況下的最短路徑樹的高度應該遠遠小於 |v|-1,在此情況下,多餘最短路徑樹高的疊代遍數就是時間上的浪費,由此,可以依次來實施最佳化。
從細節上分析,如果在某一遍疊代中,算法描述中第7行的鬆弛操作未執行,說明該遍疊代所有的邊都沒有被鬆弛。可以證明(怎么證明?):至此後,邊集中所有的邊都不需要再被鬆弛,從而可以提前結束疊代過程。這樣,最佳化的措施就非常簡單了。
設定一個布爾型標誌變數 relaxed,初值為false。在內層循環中,僅當有邊被成功鬆弛時,將 relaxed 設定為true。如果沒有邊被鬆弛,則提前結束外層循環。這一改進可以極大的減少外層循環的疊代次數。最佳化後的 bellman-ford函式如下。
這樣看似平凡的最佳化,會有怎樣的效果呢?有研究表明,對於隨機生成數據的平均情況,時間複雜度的估算公式為
1.13|E| if |E|<|V|
0.95*|E|*lg|V| if |E|>|V|
最佳化後的算法在處理有負權迴路的測試數據時,由於每次都會有邊被鬆弛,所以relaxed每次都會被置為true,因而不可能提前終止外層循環。這對應了最壞情況,其時間複雜度仍舊為O(VE)。
最佳化後的算法的時間複雜度已經和用二叉堆最佳化的Dijkstra算法相近了,而編碼的複雜程度遠比後者低。加之Bellman-Ford算法能處理各種邊值權情況下的最短路徑問題,因而還是非常優秀的。