起源
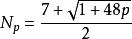七色定理人類在企圖證明四色定理過程中，發現了在曲面上作圖，反而更加容易。1974年德國的林格和美國的楊斯證明了：(公式來自《圖論導引》214頁，機械工業出版社)
P是指這個曲面的洞的個數，又叫虧格。當虧格為1時
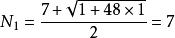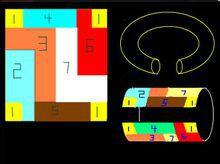
七色定理外國數學家並且給出了這個需要7種顏色染色的圖形：（參見右圖）上下對摺，再左右對摺，形成一個汽車輪胎形狀，就是有7個區域兩兩相連。
表明：在有一個洞的曲面上染色，6種顏色是不夠的。如果能夠將一個圖G畫在平面上，使得他的邊僅僅在端點相交，則稱這個圖是可以嵌入平面的，或者稱其為平面圖。
證明
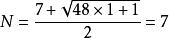七色定理又叫Heawood定理：Np=[(7+√1+48P)/2].證明這個公式，數學家用了78年。P是指這個曲面的洞的個數，又叫虧格。當虧格為3時：（公式來源：
介紹
需要7種顏色染色的圖形：下圖是全景圖，上圖：上下對摺，再左右對摺，形成一個汽車輪胎形狀，就是有7個區域兩兩相連。
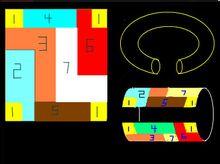環面打開後的平面圖表明：在有一個洞的曲面上染色，6種顏色是不夠的。
七色定理依據圖片製作的模型正面
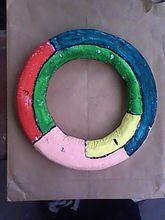模型背面疑問
Heawood的文章不僅僅指出了Kempe的錯誤，而且也給出了五色定理的一個證明，然而他沒有停留於此，Heawood繼續考慮其它一些想法，Heawood文章的主要後續成果是征對於可嵌入到球面的圖的最大色數問題。
Heawood把注意力轉移到其它曲面上圖的色數確定問題上。
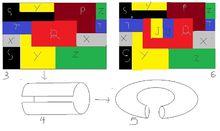七色環面疑問圖左邊圖3是一個七色環面圖，如果把中間的Q國分裂成為3個國家J國U國，就會出現不是7個區域兩兩相連，依然需要7種顏色。因為，否定4色定理的理由也是這樣的。
否定理由
今日數學書籍
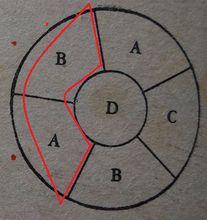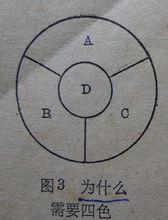
今日數學2是需要四個兩兩相連區域不需要5個兩兩相連區域的理由，是因為右圖是四個兩兩相連區域，而左圖是將右圖B區再次分為三個。破壞了兩兩相連有人需要4種顏色。
意義
區域染色的意義十分重大，在實際生活中有廣泛的套用。
