原理及證明
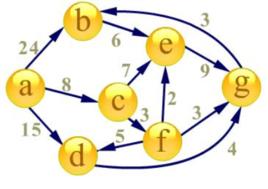
 最短路問題
最短路問題SPFA算法的全稱是:Shortest Path Faster Algorithm,是西南交通大學段凡丁於 1994 年發表的論文中的名字。不過,段凡丁的證明是錯誤的,且在 Bellman-Ford 算法提出後不久(1957 年 )已有佇列最佳化內容,所以國際上不承認 SPFA 算法是段凡丁提出的。
為了避免最壞情況的出現,在正權圖上應使用效率更高的Dijkstra算法。
若給定的圖存在負權邊,類似Dijkstra算法等算法便沒有了用武之地,SPFA算法便派上用場了。簡潔起見,我們約定加權有向圖G不存在負權迴路,即最短路徑一定存在。用數組d記錄每個結點的最短路徑估計值,而且用鄰接表來存儲圖G。我們採取的方法是動態逼近法:設立一個先進先出的佇列用來保存待最佳化的結點,最佳化時每次取出隊首結點u,並且用u點當前的最短路徑估計值對離開u點所指向的結點v進行鬆弛操作,如果v點的最短路徑估計值有所調整,且v點不在當前的佇列中,就將v點放入隊尾。這樣不斷從佇列中取出結點來進行鬆弛操作,直至佇列空為止。
定理:只要最短路徑存在,上述SPFA算法必定能求出最小值。證明:每次將點放入隊尾,都是經過鬆弛操作達到的。換言之,每次的最佳化將會有某個點v的最短路徑估計值d[v]變小。所以算法的執行會使d越來越小。由於我們假定圖中不存在負權迴路,所以每個結點都有最短路徑值。因此,算法不會無限執行下去,隨著d值的逐漸變小,直到到達最短路徑值時,算法結束,這時的最短路徑估計值就是對應結點的最短路徑值。
實際上,如果一個點進入佇列達到n次,則表明圖中存在負環,沒有最短路徑。
段凡丁論文中的複雜度證明 (O(kE),k 是小常數)是錯誤的,在此略去。該算法的最壞複雜度為 O(VE)。
對SPFA的一個很直觀的理解就是由無權圖的BFS轉化而來。在無權圖中,BFS首先到達的頂點所經歷的路徑一定是最短路(也就是經過的最少頂點數),所以此時利用數組記錄節點訪問可以使每個頂點只進隊一次,但在帶權圖中,最先到達的頂點所計算出來的路徑不一定是最短路。一個解決方法是放棄數組,此時所需時間自然就是指數級的,所以我們不能放棄數組,而是在處理一個已經在佇列中且當前所得的路徑比原來更好的頂點時,直接更新最優解。
SPFA算法有兩個最佳化策略SLF和LLL——SLF:Small Label First 策略,設要加入的節點是j,隊首元素為i,若dist(j)<dist(i),則將j插入隊首,否則插入隊尾; LLL:Large Label Last 策略,設隊首元素為i,佇列中所有dist值的平均值為x,若dist(i)>x則將i插入到隊尾,查找下一元素,直到找到某一i使得dist(i)<=x,則將i出隊進行鬆弛操作。SLF 和 LLF 在隨機數據上表現優秀,但是在正權圖上最壞情況為 O(VE),在負權圖上最壞情況為達到指數級複雜度。
代碼形式
偽代碼
SPFA實際上是Bellman-Ford基礎上的佇列最佳化
一種偽代碼
一種更容易讀懂的偽代碼:
C++代碼
pascal代碼
比較
與bfs算法比較,複雜度相對穩定。但在稠密圖中複雜度比迪傑斯特拉算法差。
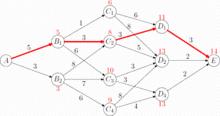
解決實際問題
2016年秋季大學先修課考試 F
poj 1502:MPI Maelstrom