Ap 權

Ap 權

正文

保證某些運算元在加權勒貝格空間Lp有界的權函式。設T是Lp(Rn)到Lp(Rn)的有界運算元,即對任意ƒ∈Lp(Rn)，有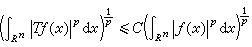

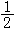
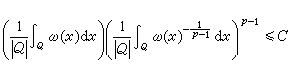式中C與ƒ無關, 積分中的dx為勒貝格測度。設ω(x)≥0是定義在Rn上的局部可積函式。問題是ω(x)滿足什麼樣的條件，可保證運算元T是Lp(Rn,ω(x)dx)到Lp(Rn,ω(x)dx)的有界運算元,即對任意ƒ∈Lp(Rn,ω(x)dx),有

式中C與ƒ無關。1972年B.穆肯霍普特提出了下面的Ap條件。所謂ω(x)滿足Ap條件(1<p<∞)是指存在常數C，使不等式

(1)

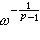對Rn中所有的方塊Q成立。這條件的意思是ω在Q的平均值與在Q 的平均值的p-1次冪的乘積是有界的。對p=1，所謂ω(x)滿足A1條件，是指不等式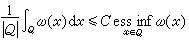

對Rn中的所有方塊Q成立,式中C與Q無關。這意思是ω(x)在Q的平均值可以被ω(x)在Q的本性下界控制。這是等式(1)的極限情形。
最後，所謂ω(x)滿足A∞條件，是指存在常數C與δ>0，使得對Rn中的任意方塊Q以及Q中的任意勒貝格可測集E，有

,

式中｜E｜表示 E的勒貝格測度。這條件的意思是指用ω(x)dx定義的測度，與勒貝格測度在某種意義下是可比較的。如果ω(x)滿足Ap條件,就說ω(x)是一個Ap權。全體Ap權構成的函式集合也用Ap表示。1972年，穆肯霍普特首先證明了，若 T是哈代-李特爾伍德極大函式M,即

，

則M(ƒ)是Lp(Rn,ω(x)dx)到Lp(Rn,ω(x)dx)的有界運算元的充分必要條件是ω是Ap權(1<p<∞)。後來,R.A.亨特、穆肯霍普特、R.L.惠登、R.R.科伊夫曼與C.費弗曼等人證明了,一般的考爾德倫-贊格蒙奇異積分運算元是Lp(Rn,ω(x)dx)到Lp(Rn,ω(x)dx),有界運算元的充分必要條件也是ω為Ap權(1<p<∞)。
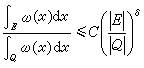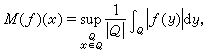上述結果對p=1與p=∞並不成立,但A1、A∞在有關理論中也是兩類十分重要的權函式。它們與Ap有密切的關係。粗略地說就是，A1是全體Ap的公共部分，而A∞是包含全體Ap的最小集合。用符號寫出來就是

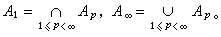
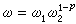　P.瓊斯於 1980年證明了Ap權的分解定理。這就是，設1<p<∞, 則ω∈Ap的充分必要條件是，其中ω1,ω2∈A1。這就有可能把對Ap問題的討論歸結為A1。
Ap權與哈代-李特爾伍德極大函式，BMO空間等有密切聯繫。例如,設ƒ是任意的局部可積函式,M(ƒ)是它的哈代－李特爾伍德極大函式，0<δ<1,則(M(ƒ))δ∈A1。又如，設b是Rn的局部可積函式,則b∈BMO的充分必要條件是存在ε>0，使得eεb∈A2。
Ap權具有一個很重要的性質，即它滿足反向赫爾德不等式：若ω∈Ap,1≤p<∞，則存在δ>0與常數C,使得

對Rn中的所有方塊Q成立。這一性質在近代偏微分方程理論中有重要的套用。
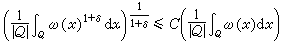
Ap權是近代調和分析的一個重要工具。
參考書目
　B. Muckenhoupt, Weighted Norm Inequalities for the Hardy Maximal function,(Trans.Amer.math.Soc.Vol.165,pp.207～226,1972.
　R.R.Coifman and C.feferman, Weighted Norm Inequalities ƒor Maximal functions and Singular Integrals,Studia Math.,Vol.51,pp.241～250,1974.

配圖

相關連線