正文
基於馬爾可夫過程理論的隨機動態系統的最優決策過程，英文縮寫 MDP。馬爾可夫決策過程是序貫決策的主要研究領域。它是馬爾可夫過程與確定性的動態規劃相結合的產物，故又稱馬爾可夫型隨機動態規劃，屬於運籌學中數學規劃的一個分支。馬爾可夫決策過程是指決策者周期地或連續地觀察具有馬爾可夫性的隨機動態系統，序貫地作出決策。即根據每個時刻觀察到的狀態，從可用的行動集合中選用一個行動作出決策，系統下一步（未來）的狀態是隨機的，並且其狀態轉移機率具有馬爾可夫性。決策者根據新觀察到的狀態，再作新的決策，依此反覆地進行。馬爾可夫性是指一個隨機過程未來發展的機率規律與觀察之前的歷史無關的性質。馬爾可夫性又可簡單敘述為狀態轉移機率的無後效性。狀態轉移機率具有馬爾可夫性的隨機過程即為馬爾可夫過程。馬爾可夫決策過程又可看作隨機對策的特殊情形，在這種隨機對策中對策的一方是無意志的。馬爾可夫決策過程還可作為馬爾可夫型隨機最優控制，其決策變數就是控制變數。
發展概況50年代R.貝爾曼研究動態規劃時和L.S.沙普利研究隨機對策時已出現馬爾可夫決策過程的基本思想。R.A.霍華德(1960)和D.布萊克韋爾(1962)等人的研究工作奠定了馬爾可夫決策過程的理論基礎。1965年，布萊克韋爾關於一般狀態空間的研究和E.B.丁金關於非時齊（非時間平穩性）的研究，推動了這一理論的發展。1960年以來，馬爾可夫決策過程理論得到迅速發展，套用領域不斷擴大。凡是以馬爾可夫過程作為數學模型的問題，只要能引入決策和效用結構，均可套用這種理論。
數學描述周期地進行觀察的馬爾可夫決策過程可用如下五元組來描述：{
，(
(
)，
∈
},其中
為系統的狀態空間（見狀態空間法）；
(
)為狀態
(
∈
)的可用行動（措施，控制）集；
為時齊的馬爾可夫轉移律族，族的參數是可用的行動；
是定義在Γ(Г呏{(
):
∈
(
)，
∈
}上的單值實函式；若觀察到的狀態為
，選用行動
，則下一步轉移到狀態
的機率為
(
│
)，而且獲得報酬γ(
),它們均與系統的歷史無關；
是衡量策略優劣的指標（準則）。
策略策略是提供給決策者在各個時刻選取行動的規則，記作
＝(
，
，
，…，
，
…)，其中
是時刻
選取行動的規則。從理論上來說，為了在大範圍尋求最優策略
，最好根據時刻
以前的歷史，甚至是隨機地選擇最優策略。但為了便於套用，常採用既不依賴於歷史、又不依賴於時間的策略，甚至可以採用確定性平穩策略。
指標衡量策略優劣的常用指標有折扣指標和平均指標。折扣指標是指長期折扣〔把
時刻的單位收益折合成0時刻的單位收益的
(
<1)倍〕期望總報酬。平均指標是指單位時間的平均期望報酬。採用折扣指標的馬爾可夫決策過程稱為折扣模型。業已證明：若一個策略是
折扣最優的，則初始時刻的決策規則所構成的平穩策略對同一
也是折扣最優的，而且它還可以分解為若干個確定性平穩策略，它們對同一
都是最優的。現在已有計算這種策略的算法。採用平均指標的馬爾可夫決策過程稱為平均模型。業已證明：當狀態空間
和行動集
(
)均為有限集時，對於平均指標存在最優的確定性平穩策略；當
和（或）
(
)不是有限的情況,必須增加條件，才有最優的確定性平穩策略。計算這種策略的算法也已研製出來。
數學描述
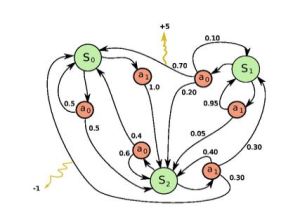馬爾可夫決策過程