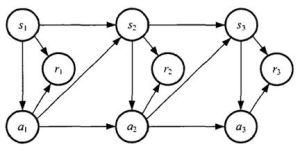
簡介
 馬爾可夫決策相關書籍
馬爾可夫決策相關書籍研究一類可周期地或連續地進行觀察的隨機動態系統的最最佳化問題。在各個時刻根據觀察到的狀態,從它的允許決策(控制、行動、措施等)集合中選用一個決策而決定了系統下次的轉移規律與相應的運行效果。並假設這兩者都不依賴於系統過去的歷史。在各個時刻選取決策的目的,是使系統運行的全過程達到某種最優運行效果,即選取控制(影響)系統發展的最優策略。 馬爾可夫決策過程是指決策者周期地或連續地觀察具有馬爾可夫性的隨機動態系統,序貫地作出決策。即根據每個時刻觀察到的狀態,從可用的行動集合中選用一個行動作出決策,系統下一步(未來)的狀態是隨機的,並且其狀態轉移機率具有馬爾可夫性。決策者根據新觀察到的狀態,再作新的決策,依此反覆地進行。馬爾可夫性是指一個隨機過程未來發展的機率規律與觀察之前的歷史無關的性質。馬爾可夫性又可簡單敘述為狀態轉移機率的無後效性。狀態轉移機率具有馬爾可夫性的隨機過程即為馬爾可夫過程。馬爾可夫決策過程又可看作隨機對策的特殊情形,在這種隨機對策中對策的一方是無意志的。馬爾可夫決策過程還可作為馬爾可夫型隨機最優控制,其決策變數就是控制變數。
發展概況
50年代R.貝爾曼研究動態規劃時和L.S.沙普利研究隨機對策時已出現馬爾可夫決策過程的基本思想。R.A.霍華德(1960)和D.布萊克韋爾(1962)等人的研究工作奠定了馬爾可夫決策過程的理論基礎。1965年,布萊克韋爾關於一般狀態空間的研究和E.B.丁金關於非時齊(非時間平穩性)的研究,推動了這一理論的發展。1960年以來,馬爾可夫決策過程理論得到迅速發展,套用領域不斷擴大。凡是以馬爾可夫過程作為數學模型的問題,只要能引入決策和效用結構,均可套用這種理論。
數學描述
周期地進行觀察的馬爾可夫決策過程可用如下五元組來描述:{S,A(i),i∈S,q,γ,V},其中S 為系統的狀態空間(見狀態空間法); A(i)為狀態i(i∈S)的可用行動(措施,控制)集;q為時齊的馬爾可夫轉移律族,族的參數是可用的行動;γ是定義在Γ(Г呏{(i,ɑ):a∈A(i),i∈S}上的單值實函式;若觀察到的狀態為i,選用行動a,則下一步轉移到狀態 j的機率為q(j│i,ɑ),而且獲得報酬γ(j,ɑ),它們均與系統的歷史無關;V是衡量策略優劣的指標(準則)。
策略
策略是提供給決策者在各個時刻選取行動的規則,記作π=(π0,π1,π2,…, πn,πn+1…),其中πn是時刻 n選取行動的規則。從理論上來說,為了在大範圍尋求最優策略πn,最好根據時刻 n以前的歷史,甚至是隨機地選擇最優策略。但為了便於套用,常採用既不依賴於歷史、又不依賴於時間的策略,甚至可以採用確定性平穩策略。
指標
衡量策略優劣的常用指標有折扣指標和平均指標。折扣指標是指長期折扣〔把 t時刻的單位收益折合成0時刻的單位收益的βt(β < 1)倍〕期望總報酬;平均指標是指單位時間的平均期望報酬。 採用折扣指標的馬爾可夫決策過程稱為折扣模型。業已證明:若一個策略是β折扣最優的,則初始時刻的決策規則所構成的平穩策略對同一β也是折扣最優的,而且它還可以分解為若干個確定性平穩策略,它們對同一β都是最優的。現在已有計算這種策略的算法。
採用平均指標的馬爾可夫決策過程稱為平均模型。業已證明:當狀態空間S 和行動集A(i)均為有限集時,對於平均指標存在最優的確定性平穩策略;當S和(或)A(i)不是有限的情況,必須增加條件,才有最優的確定性平穩策略。計算這種策略的算法也已研製出來。
相關書籍
 《馬爾可夫決策過程引論》
《馬爾可夫決策過程引論》《實用馬爾可夫決策過程》不確定理論與最佳化叢書(不確定理論與最佳化叢書)
內容簡介:馬爾可夫決策過程是研究隨機環境下多階段決策過程最佳化問題的理論工具,在過去的幾十年中,隨著生態科學、經濟理論、通訊工程以及眾多學科中需要考慮不確定因素和序列決策問題的大量新模型的湧現,進一步刺激了馬爾可夫決策過程在理論上和套用領域中長足發展。 本書從簡單的例子開始,介紹了馬爾可夫決策過程的基本概念、決策過程以及一些常用的基本理論。還介紹了多種最優準則,包括有限階段準則、折扣準則、平均準則、權重報酬準則、機率準則等。從模型角度考慮了有限狀態空間、可數狀態空間和一般Borel狀態空間;從決策時間上來說,考慮了離散時間、連續時間和半馬氏決策時刻問題。本文還介紹了大量的套用實例以及建模方法。本書可作為高年級大學和研究生教材,也可作為運籌學、管理科學、信息科學、系統科學以及計算機科學和工程領域的學者和技術人員的參考書。運籌學已被廣泛套用於工商企業、軍事部門、民政事業等研究組織內的統籌協調問題,故其套用不受行業、部門之限制;運籌學既對各種經營進行創造性的科學研究,又涉及到組織的實際管理問題,它具有很強的實踐性,最終應能向決策者提供建設性意見,並應收到實效;它以整體最優為目標,從系統的觀點出發,力圖以整個系統最佳的方式來解決該系統各部門之間的利害衝突。對所研究的問題求出最優解,尋求最佳的行動方案,所以它也可看成是一門最佳化技術,提供的是解決各類問題的最佳化方法。
相關人物
馬爾可夫,1856年6月14日生於梁贊,1922年7月20日卒於聖彼得堡。1874年入聖彼得堡大學,受P.L.切比雪夫思想影響很深。1878年畢業,並以《用連分數求微分方程的積分》一文獲金質獎章。兩年後,取得碩士學位 ,並任聖彼得堡大學副教授。1884年取得物理-數學博士學位,1886 年任該校教授。1896年被選為聖彼得堡科學院院士。1905年被授予功勳教授稱號。 馬爾可夫是彼得堡數學學派的代表人物。以數論和機率論方面的工作著稱。他的主要著作有《機率演算》等。在數論方面,他研究了連分數和二次不定式理論 ,解決了許多難題 。在機率論中,他發展了矩法,擴大了大數律和中心極限定理的套用範圍。馬爾可夫最重要的工作是在1906~1912年間,提出並研究了一種能用數學分析方法研究自然過程的一般圖式——馬爾可夫鏈。同時開創了對一種無後效性的隨機過程——馬爾可夫過程的研究。馬爾可夫經多次觀察試驗發現,一個系統的狀態轉換過程中第n次轉換獲得的狀態常決定於前一次(第(n-1)次)試驗的結果。
馬爾可夫進行深入研究後指出:對於一個系統,由一個狀態轉至另一個狀態的轉換過程中,存在著轉移機率,並且這種轉移機率可以依據其緊接的前一種狀態推算出來,與該系統的原始狀態和此次轉移前的馬爾可夫過程無關。馬爾可夫鏈理論與方法已經被廣泛套用於自然科學、工程技術和公用事業中。