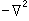電磁場的本徵函式

電磁場的本徵函式

正文

在一定的邊界條件下，分布形式不因激勵方式而定的電磁場模式，是這種邊界條件下的本徵模式。本徵函式和本徵值是數學物理方法的基本概念之一，是表達本徵模式的數學工具，在電磁場模式分析中十分重要，而模式分析則是解給定源的場的有效方法之一。近代數學已把本徵函式和本徵值的研究推進到了新的深度和廣度。
對於線性運算元 L，如果其定義域為某類函式（例如在邊界上為零或邊界上法嚮導數為零，而在場區域內二階導數連續且平方可積的函式）,則此類中的函式u和常數λ,如能滿足方程Lu＝λu,就分別稱為運算元 L在這函式類中的本徵函式和本徵值。在靜態場和簡諧場中常遇到的運算元是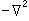。例如在ɑ×b矩形域中,二維運算元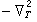滿足在邊界上為零條件的本徵函式是 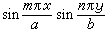（m、n都是正整數）,而滿足在邊界上法嚮導數為零條件的本徵函式則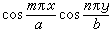（m、n都是正整數，有一個可以為零）,二者相應的本徵值都是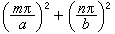。二維運算元 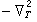的這些本徵函式可以表達靜態場或簡諧場在矩形柱區域中橫向分布的本徵模式。
例如，在均勻填充介質的波導中，簡諧電磁場除可能有橫電磁(TEM)模式外，還有E模（縱向磁場為零）和H 模（縱向電場為零）兩類模式（見電磁波模式）。取管軸為z坐標軸，這兩類模式的一般表達式為

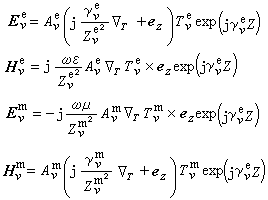
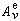式中足標ν為模式的標號，常為二元有序整數組；和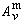為任意常數;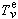為二維運算元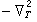滿足在邊界上為零條件的本徵函式;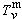為滿足在邊界上法嚮導數為零條件的本徵函式;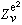和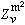則是相應的本徵值,恆為正實數，分別構成無窮序列；常數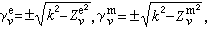它們可能為實數（能傳播的情形）或虛數（消失衰減的情形）。
在波導管內介質有縱向間斷面的情形中，除 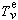或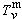在間斷面橫截線上保持常數的模式外,E模與H模必然混合存在。這時應從上述兩類函式中各取一個構成本徵函式對，而且在不同的地區應取不同的函式對。它們除分別滿足管壁上的邊界條件外，還應保證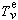、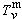以及Eν和Hν的切向分量在介質界面上都是連續的。相應地，在同一介質區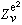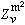＝,而在不同介質區則取不同的值，以保證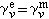對每一模式為定值。
在已知的各種正交柱坐標系中，只在直線、圓柱、橢圓柱、拋物柱坐標系中，能用分離變數法求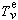和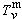。但只在一些管壁和介質間斷面形狀簡單的情形可以列出本徵值滿足的函式方程。一般需套用適當的方法求近似解。
在場區橫向延至無限遠的情形（如介質柱內外或導體柱以外）中,除某些特殊情形,如介質柱有相當粗（或導體柱面上敷有相當厚的介質層），可能存在有限個本徵函式(表達表面波的橫向分布)外，一般不存在本徵函式。儘管在這些情況中可能找到既滿足方程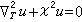，又滿足邊界條件的函式，可是它們非平方可積（相當於能流為無窮大），所以它們不能表達本徵模式。
在均勻填充介質的柱形諧振腔內，場需同時滿足側壁和端面上的邊界條件。其中Z分量的邊界條件為(en指向側壁法向)

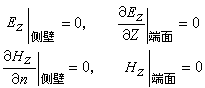
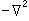這時，本徵模的EZ和HZ應為三維運算元在滿足上述邊界條件的函式類中的本徵函式，波數平方k2則應等於相應的本徵值。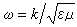就是腔的自由振盪頻率。例如在ɑ×b×c 矩形腔內，本徵值的通式為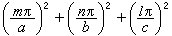

m、n、l都是正整數，可能有一個為零。
在其他形式的導體腔內，需研究矢量方程

在相應邊界條件下的解。在圓球形腔中，可以依照

Hr＝0（E模）和 Er＝0（H模）

而分為兩種模式，分別用標量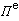和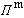(稱為德拜勢)來表示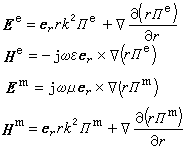

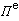其中和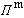應滿足亥姆霍茲方程。
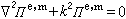在球形導體表面,德拜勢應滿足邊界條件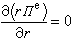和Πm＝0。因此,在球形腔內,Πe和Πm應取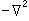運算元在滿足上列邊界條件且二階導數連續並平方可積函式類中的本徵函式，而k2則為相應的本徵值。
參考書目
　林為乾:《微波理論與技術》,科學出版社,北京,1979。
　M.博恩和E.沃爾夫著,楊葭蓀等譯《光學原理》,科學出版社,北京，1978。(M.Born and 　E.Wolf,Principles　of OPtics,Pergamon Press,Oxford,1975.)
　D.S. Jones,Methods　in　Electromagnetic　Wave　Propagation,Clarendon Press,Oxford,1979.

配圖

相關連線