概念
定義
含有未知函式的等式叫做函式方程。如f(x+1)=x、f(－x)=f(x)、f(－x)= －f(x)、f(x+2)=f(x)等。其中f(x)是未知函式
解
能使函式方程成立的函式叫做函式方程的解。如f(x)=x－1、偶函式、奇函式、周期函式分別是上述各方程的解
解函式方程
函式方程與代數方程、微分方程不同，並沒有普遍的解法。所以這個分支也沒能發展起來。如上述的解為Gamma函式和初等函式的方程的解法完全不同。
對於二元函式方程，對其變數賦予特殊值的做法較多。
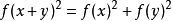函式方程例子：解函式方程。
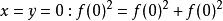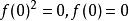函式方程
函式方程設。所以。
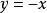函式方程現在，設：
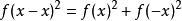函式方程
函式方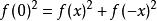程
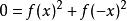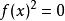函式方程
函式方程由於實數的平方非負，以及兩個非負數的和為零若且唯若兩個數都為零，因此對於所有 x，，所以f(x)=0是唯一的解。
定理
若f(x)是單調（或連續）函式且滿足f(x+y)=f(x)+f(y) (x,y∈R)、則f(x)=xf(1)
證明：由題設不難得
f(x+x+…+x)=f(x)+f(x)+…+f(x)
取x=x=…=x=x，得f(nx)=nf(x) (n∈N+)
令x=0，則f(0)=nf(0)，解得f(0)=0 --------- （1）
x=1，則f(n)=nf(1)
x=m/n，則f(m)=nf(m/n) ，解得f(m/n)= f(m)/n= mf(1)/n --------- (2)
x=－m/n ，且令y=－x>0，則f(x)+f(y)=f(x+y)=f(0)=0
∴f(x)=－f(y)=－yf(1)=xf(1) (m,n∈N+,且(m,n)=1) ---------(3)
由上述（1）（2）（3）知：對任意有理數x均有f(x)=xf(1)
另一方面，對於任意的無理數x，因f(x)連續，取以x為極限的有理數序列，則有 ：f(x)= f(xn)= xnf(1)=xf(1)
綜上所述，對於任意實數x，有
f(x)=xf(1)
解法
代換法
把函式方程中的自變數適當地以別的自變數代換（代換時應注意使函式的定義域不會發生變化），得到一個新的函式方程，然後設法求得未知函式
例1 （1）已知f(2x－1)=x2+x，那么f(x)=______________。
略解：設t=2x－1，則x= (t+1)/2，那么f(t)= [(t+1) ]/4+ (t+1)/2=(t +4t+3)/4
故f(x)=(x +4x+3)/4
(2) 已知f(x+1)=x+2 ，那么f(x)=____________。
略解：f(x+1)=(x+1) －1，故f(x)=x －1 (x≥1)
(3) 已知f(x+2)=x +2，那么f(x)=_______________。
略解：f(x+2)=(x+2) －2，故f(x)=x －2 (|x|≥2)
例2 設ab≠0,a ≠b ，求af(x)+bf(-t)=cx的解
解：分別用x=-t，x=t代入已知方程，得
af(-t)+bf(t)=-ct------(1)
af(t)+bf(-t)=ct------(2)
由（1）（2）組成方程組解得 f(t)=ct/a-b
即： f(x)=cx/a-b
待定係數法
當函式方程中的未知數是多項式時，可用此法經比較係數而得
例3 已知f(x)是一次函式，且f{f[f...f(x)]}=1024x+1023。求f(x)
解：設f(x)=ax+b (a≠0)，記f{f[f…f(x)]}=fn(x)，則
n次
f (x)=f[f(x)]=a(ax+b)+b=a x+b(a+1)
f (x)=f{f[f(x)]}=a[a x+b(a+1)]+b=a x+b(a +a+1)
依次類推有：f (x)=a x+b(a +a +…+a+1)=a x+...
由題設知：
a =1024
∴a=2，b=1 或 a=－2，b=－3
∴f(x)=2x+1 或 f(x)=－2x－3
疊代法
由函式方程找出函式值之間的關係，通過n次疊代得到函式方程的解法
例4 設f(x)定義在正整數集上，且f(1)=1,f(x+y)=f(x)+f(y)+xy。求f(x)
解：令y=1，得f(x+1)=f(x)+x+1
再依次令x=1,2,…,n－1，有
f(2)=f(1)+2
f(3)=f(2)+3
……
f(n－1)=f(n－2)+(n－1)
f(n)=f(n－1)+n
依次代入，得
f(n)=f(1)+2+3+…+(n－1)+n=
∴f(x)= n(n+1)/2
(x∈N+)
例5 ，已知f(1)= 且當n>1時有 。求f(n) (n∈N+)
解：把已知等式（遞推公式）進行整理，得
f(n－1)－f(n)=2(n+1)f(n)f(n－1)
∴ =2(n+1)
把n依次用2,3,…,n代換，得(n－1)個等式相加，得
=2[3+4+…+(n+1)]=(n－1)(n+4)
∴ f(n)= (n－1)(n+4)=n +3n+1
∴f(n)=n +3n+1
柯西法
在f(x)單調（或連續）的條件下，利用柯西函式方程的解求解
例6 設f(x)連續且不恆為0，求函式方程f(x+y)=f(x)f(y)的解
解：∵f(x)=f(x+y)=f(x)f(y)≥0
若存在x0∈R，使f(x0)=0。則對一切實數x，有
f(x)=f(x－x0+x0)=f(x－x0)f(x0)=0
這與f(x)不恆為0矛盾，故f(x)>0
對題設f(x+y)=f(x)f(y)兩邊取自然對數，得
㏑f(x+y)=㏑f(x)f(y)
∴㏑f(x+y)=㏑f(x)+㏑f(y)
令g(x)=㏑f(x)
∵f(x)>0且連續 ∴g(x)連續且滿足g(x+y)=g(x)+g(y)。由定理知：
g(x)=g(1)x
故 ㏑f(x)=x㏑f(1)
∴f(x)=e ㏑f(1)=f(1)^x
令f(1)=a，則f(x)=a (a>0)
類似的，利用柯西函式方程的解，在連續或單調的條件下可得：
（1） 若f(xy)=f(x)+f(y) (x>0,y>0)，則f(x)=㏒ax
（2） 若f(xy)=f(x)f(y) (x>0,y>0)，則f(x)=ux(u由初值給出)
（3） 若f(x+y)=f(x)+f(y)+kxy，則f(x)=ax +bx
（4） 若f(x+y)+f(x－y)=2f(x)，則f(x)=ax+b
例子
函式方程
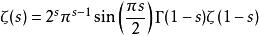函式方程的解是黎曼ζ函式。
函式方程
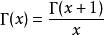函式方程的解是伽瑪函式。
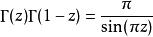函式方程
函式方程的解是伽瑪函式。
