介紹
拓撲學是一門十分重要的基礎性的數學分支，它的許多概念、理論和方法在數學的其他分支有著廣泛的套用，有的甚至已成為通用語言。拓撲學有多個研究方向，如一般拓撲學、代數拓撲學、微分拓撲學，低維流形等。離散拓撲空間是點集拓撲學中一種最簡單的拓撲空間，但是它對於整個拓撲學脈絡的理解起著非常重要的作用。
預備知識
定義1設X是一個集合，T是X的一個子集族。如果T滿足如下條件：
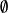離散拓撲① X， ∈T；
②若A，B∈T，則A∩B∈T；
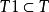離散拓撲③若 ，則∪ A∈T1A∈T；
則稱T是X的一個拓撲。
如果T是集合X的一個拓撲，則X叫做拓撲T的空間，偶對(X，T) 是一個拓撲空間。在不引起混淆或無須指出拓撲時，直接稱X是拓撲空間。此外，T的每一個元素都叫做拓撲空間(X，T) 或X中的一個開集。
定義2設X是一個集合。令T = P(x) ，即由X的所有子集構成的族。由定義1可知T是X的一個拓撲，稱為X的離散拓撲，並且稱(X，T) 為一個離散拓撲空間。在離散拓撲空間(X，T) 中，X的每一個子集都是開集。
概念性質
離散拓撲(discrete topology)一類特殊的拓撲。設X為任意非空集合，則由X的所有子集組成的拓撲稱為X上的離散拓撲。它是X上的最細拓撲。由此得到的拓撲空間稱為離散拓撲空間或離散空間。
離散拓撲若X為離散空間，則X的任意點都是孤立點。若A是X的任意子集，則A是X的既開又閉的集，並且A的邊界為空集。在X上定義的任意映射都是連續的。離散空間恆可度量化，它滿足一切分離公理，是局部緊空間，是第一可數空間。多於一點的離散空間是局部連通的但不是連通的，也不是道路連通的。離散拓撲分有限離散拓撲、可數離散拓撲和不可數離散拓撲三類。根據X分別是有限集、可數集和不可數集，容易給出它們的定義。它們的拓撲性質也不盡相同，如有限離散拓撲是緊、可數緊、序列緊的，其他二者不是。而不可數離散拓撲不是可分的、第二可數的、 緊的、林德勒夫的，其他二者卻是。
空間性質
性質1集合X的離散拓撲T是X的最大拓撲，即對X的每一個拓撲T1，均有。
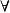離散拓撲證明 由拓撲T1的定義可得： 對 A∈T1，有A∈ P(x)。此外，T是X的離散拓撲意味著T =P(x) ，因此，A∈T，從而由A的任意性可知。
性質2離散拓撲空間(X，T) 中：
離散拓撲①點x的鄰域系是Ux= A X | x∈ A}，即凡是X的包含x的子集都是x的鄰域。
② X的每一個子集既開又閉。
離散拓撲 離散拓撲證明 對任意的x∈X，有{x}∈P(x)= T，故{x} 是開集。另外，對任意的x ∈ A X，有x∈{x} A，從而由鄰域的定義可知A是X的鄰域。
離散拓撲設A是X中的任一子集，那么有A∈P(x)=T，即A是開集。另一方面，由X ～ AX可得Ac∈P(x)= T， 故A是閉集。
註： 一般拓撲空間的子集也可能是既不開也不閉的。
離散拓撲 離散拓撲性質3離散拓撲空間(X，T) 中，若AX，則A的導集A' = ，即A中不含有任何一個聚點。
離散拓撲 離散拓撲證明 對任意的x∈X，存在x的一個開鄰域{x} ，使得{x}∩(A －{x} )= ，從而x不是A的聚點，因此，由x的任意性可得：集合A中不含有任何一個聚點，即A' = 。
