定義
在拓撲學中,帶有 密著拓撲(trivial topology)的拓撲空間是其中僅有的開集是空集和整個空間的空間。這種空間有時叫做 不可分空間(indiscrete space),它的拓撲有時叫做 不可分拓撲。在直覺上,這有著所有點都被“粘著在一起”而通過拓撲方式不可區分的推論。
密著拓撲是有最小可能數的開集的拓撲,因為拓撲的定義只要求兩個集合是開集。儘管簡單,帶有多於一個元素的密著拓撲空間缺乏關鍵的性質:它不是T空間。
操作案例
 密著拓撲
密著拓撲密著拓撲屬於偽度量空間,在其中任何兩點之間的距離是 0,並屬於一致空間,在其中全體笛卡爾乘積是 是僅有的周圍。
 密著拓撲
密著拓撲 密著拓撲
密著拓撲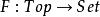 密著拓撲
密著拓撲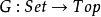 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲設 是帶有連續映射的拓撲空間範疇,和 是帶有函式的集合範疇。如果 是指派每個拓撲空間到它的底層集合的函子(所謂的遺忘函子),並且 是把密著拓撲放置到給定集合上的函子,則 右伴隨於 。(把離散拓撲放置到給定集合上的函子 左伴隨於 。)
基本原理
在拓撲學中,帶有密著拓撲(trivial topology)的拓撲空間是其中僅有的開集是空集和整個空間的空間。這種空間有時叫做不可分空間(indiscrete space),它的拓撲有時叫做不可分拓撲。在直覺上,這有著所有點都被“粘著在一起”而通過拓撲方式不可區分的推論。
 密著拓撲
密著拓撲不可分空間 的其他性質包括:
 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲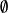 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲唯一的閉集是空集和 。 的唯一可能的基是 。 如果 有多於一個點,則由於它不是 T0,它不滿足任何更高的T 公理。特別是,它不是豪斯多夫空間。不是豪斯多夫的, 就不是序拓撲,也不是可度量的。 但是 是正則空間、完全正則空間、正規空間和完全正規空間;儘管是在非常空洞意義上,因為僅有的閉集是 和 。 是緊緻空間因此是仿緊緻空間、林德勒夫空間和局部緊緻空間。 所有定義域是拓撲空間而陪域是 的函式都是連續函式。 是道路連通並因此是連通空間。
 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲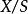 密著拓撲
密著拓撲 密著拓撲
密著拓撲是第一可數空間、第二可數空間和可分離空間。 所有 的子空間都有密著拓撲。 所有 的商空間都有密著拓撲。 密著拓撲空間的任意乘積,帶有要么乘積拓撲要么盒拓撲,都有密著拓撲。 所有 中的序列都收斂於 的所有點。特別是,所有序列都有收斂子序列(整個序列),因此是 是序列緊緻。 所有集合除了 的內部都是空集。 所有 的非空子集的閉包都是 。在另一種方式下: 所有 的非空子集都是稠密的,這個性質刻畫了密著拓撲空間。 如果 是任何帶有多於一個元素的 的子集,則所有 的元素都是 的極限點。如果 是單元素集合,則所有 的點仍是 S 的極限點。 是Baire空間。 兩個承載密著拓撲的拓撲空間是同胚的,若且唯若它們有相同的勢。 在某種意義上,密著拓撲的對立者是離散拓撲,它的所有子集都是開集 。
性質
 密著拓撲
密著拓撲不可分空間 的其他性質包括:
 密著拓撲
密著拓撲1、唯一的閉集是空集和 。
 密著拓撲
密著拓撲 密著拓撲
密著拓撲2、 的唯一可能的基是 。
 密著拓撲
密著拓撲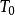 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲3、如果 有多於一個點,則由於它不是 ,它不滿足任何更高的分離公理。特別是,它不是豪斯多夫空間。不是豪斯多夫的, 就不是序拓撲,也不是可度量的。但是是正則空間、完全正則空間、正規空間和完全正規空間;儘管是在非常空洞意義上,因為僅有的閉集是 和 。
4、 是緊緻空間因此是仿緊緻空間、林德勒夫空間和局部緊緻空間。所有定義域是拓撲空間而陪域是 X的函式都是連續函式。
5、是道路連通,並因此是連通空間。
6、是第一可數空間、第二可數空間和可分離空間。
 密著拓撲
密著拓撲7、所有 的子空間都有密著拓撲。
 密著拓撲
密著拓撲8、所有 的商空間都有密著拓撲。
9、密著拓撲空間的任意乘積,帶有要么乘積拓撲要么盒拓撲,都有密著拓撲。
 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲10、所有 中的序列都收斂於 的所有點。特別是,所有序列都有收斂子序列(整個序列),因此是 是序列緊緻。
 密著拓撲
密著拓撲11、所有集合除了 的內部都是空集。
 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲12、所有 的非空子集的閉包都是 。在另一種方式下:所有 的非空子集都是稠密的,這個性質刻畫了密著拓撲空間。
 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲13、如果 是任何帶有多於一個元素的的子集,則所有 的元素都是 的極限點。如果 是單元素集合,則所有的點仍是 的極限點。
14、是Baire空間。
15、兩個承載密著拓撲的拓撲空間是同胚的,若且唯若它們有相同的勢。
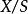 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲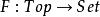 密著拓撲
密著拓撲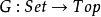 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲 密著拓撲
密著拓撲在某種意義上,密著拓撲的對立者是離散拓撲,它的所有子集都是開集。密著拓撲屬於偽度量空間,在其中任何兩點之間的距離是0,並屬於一致空間,在其中全體笛卡爾乘積是 是僅有的周圍。設 是帶有連續映射的拓撲空間範疇,和 是帶有函式的集合範疇。如果 是指派每個拓撲空間到它的底層集合的函子(所謂的遺忘函子),並且 是把密著拓撲放置到給定集合上的函子,則 右伴隨於 。(把離散拓撲放置到給定集合上的函子 左伴隨於。)

