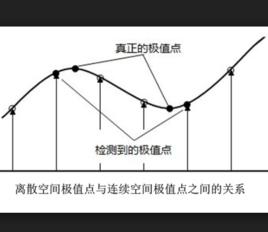
定義
給定集合 X:
在 X上的 離散拓撲是通過集合 X的所有子集是開集而定義的,而 X是 離散拓撲空間,如果它配備了它的離散拓撲;
在 X上的 離散一致是通過設定 X× X中的對角{( x, x): x∈ X}的所有超集為周圍(entourage)而定義的,而 X是 離散一致空間,如果它配備了它的離散一致。
 離散空間
離散空間在 X上的 離散度量定義為
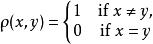 離散空間
離散空間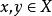 離散空間
離散空間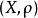 離散空間
離散空間對於任何。在這種情況下被稱為 離散度量空間或 孤點 空間。
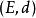 離散空間
離散空間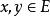 離散空間
離散空間度量空間被稱為“一致離散”的,如果存在r>0使得對於任何,要么x=y要么d(x,y)>r。在度量空間底層的拓撲空間可以是離散的,而沒有一致離散的度量:例如在實數的集合{1, 1/2, 1/4, 1/8, ...}上的平常度量。
性質
在離散度量空間上的底層一致是離散一致,而在離散一致空間上的底層拓撲是離散拓撲。因此離散空間的不同概念是相互兼容的。在另一個方面,非離散一致或度量空間的底層拓撲可以是離散的;一個例子是度量空間 X:= {1/ n: n= 1,2,3,...} (帶有從實直線繼承來的度量,並給出為d( x, y)= | x− y|)。明顯的,這不是離散度量;還有這個空間不是完備的並因襲作為一致空間不是離散的。然而它作為拓撲空間是離散的。我們稱 X是“拓撲離散”而非“一致離散”或“度量離散”。
此外還有:
•拓撲空間是離散的,若且唯若它的單元素集合是開集,也就是若且唯若他不包含任何會聚點。
•單元素集合形成了這個離散拓撲的基。
•一致空間X是離散的,若且唯若對角{(x,x):x∈X}是周圍。
•所有離散拓撲空間滿足每個分離公理;特別是,所有離散空間都是豪斯多夫空間,就是說是分離的。
•離散空間是緊緻空間,若且唯若它是有限的。
•所有離散一致或度量空間是完備空間。
•組合上兩個性質,所有離散一致或度量空間是完全有界空間,若且唯若它是有限的。
•所有離散度量空間是有界的。
•所有離散空間是第一可數空間,並且離散空間是第二可數空間若且唯若它是可數的。
•所有離散空間都是完全不連通空間。
•所有非空離散空間都是第二範疇。
•任何兩個有相同勢的離散空間都是同胚的。
任何從離散拓撲空間到另一個拓撲空間的函式是連續函式,任何從離散一致空間到另一個一致空間的函式是一致連續的。就是說,在拓撲空間和連續映射範疇中,或在一致空間和一致連續映射範疇內,離散空間 X是集合 X上的自由對象。這些性質是更廣泛現象的實例,在其中離散結構通常自由於集合上。
對於度量空間,事情更加複雜,因為依賴於所選擇的態射有很多度量空間範疇。離散度量空間當然是自由的,在態射都是一致連續映射或連續映射的時候,但是這沒有說對度量結構有價值的事情,只針對了一致或拓撲結構。與度量結構更有關的範疇可以通過把態射限制為利普希茨連續映射或短映射來找到;但是,這些範疇沒有自由對象(在多於一個元素的時候)。但是,離散度量空間在有界度量空間和利普希茨連續映射範疇內是自由的,並且它在有界於1的度量空間和短映射範疇是自由的。就是說,從離散度量空間到另一個有界度量空間的函式是利普希茨連續的,而任何從離散度量空間到另一個有界於1的度量空間的函式是短映射。
在其他方向上,從拓撲空間 Y到離散空間 X的函式 f是連續的,若且唯若它是局部常數函式,在所有 Y的點都有 f在其上的鄰域是常數的意義上。
用途
離散結構通常用做不承載任何其他自然拓撲、一致或度量的集合上“預設結構”。例如,任何群都可以通過給予它離散拓撲被認為是拓撲群,蘊涵了關於拓撲群適用於所有群的定理。實際上,分析學家更偏好被代數學家作為離散群來研究的平常的非拓撲群。在某些情況下,這可有用的套用,例如組合上Pontryagin對偶性。
0維流形(或微分流形或解析流形)就只是離散拓撲空間。在前面段落的精神下,我們可以把任何離散群看作0維李群。
儘管離散空間從拓撲學的角度看沒有什麼令人興奮的,可以卻可以從它們構造有趣的空間。例如,可數無限多個自然數離散空間的乘積同胚於無理數空間,帶有同胚給出自連分數展開。可數多個離散空間{0,1}的乘積同胚於康托爾集合;並且事實上一致同胚於康托爾集合,如果我們在乘積上使用乘積一致。這種同胚給出自數字的三進制表示。(參見康托爾空間)。
在數學基礎中,{0,1}乘積的緊緻性質的研究是超濾子原理的拓撲途徑的中心,它是弱形式的選擇公理。
不可分空間
在某種意義上,離散拓撲的對立者是密著拓撲(也叫做“不可分拓撲”),它有最少可能數目的開集(就是空集和空間自身)。這裡的離散拓撲是始對象和自由對象,而不可分拓撲是終對象或cofree對象:所有從拓撲空間到不可分空間的函式都是連續的。