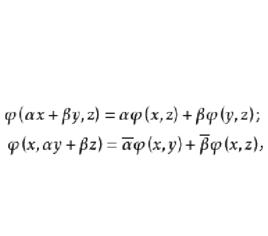基本介紹
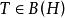雙線性形式設H是Hilbert空間，是自伴運算元，令
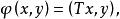雙線性形式
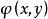雙線性形式則滿足
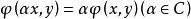雙線性形式(i)；
雙線性形式(ii)；
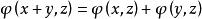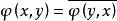雙線性形式(iii)。
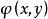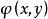雙線性形式 雙線性形式(i)和(ii)實際是說，關於第一個變元x是線性的，從(iii)知關於第二個變元y是共軛線性的，即
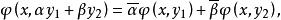雙線性形式我們可以利用上述性質給出一個更一般的概念。
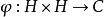雙線性形式定義1設H是Hilbert空間，如果二元映射滿足：
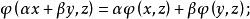雙線性形式(i)
雙線性形式(ii)，
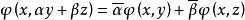雙線性形式則稱為H上的 雙線性形式。
如果條件(ii)代以更強的：
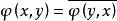雙線性形式 雙線性形式(iii)，則稱為H上 共軛的雙線性形式。
雙線性形式如果一個雙線性形式滿足：
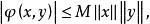雙線性形式 雙線性形式(iv) 存在M≥o，使則稱為 有界雙線性形式。
雙線性形式若雙線性形式滿足：
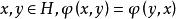雙線性形式 雙線性形式(v)對任意，則稱為 自伴雙線性形式。
雙線性形式如果共軛雙線性形式滿足：
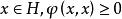雙線性形式 雙線性形式(vi)對所有的，則稱為 正定的雙線性形式。
注: 雙線性形式關於後一個變數實際上是共軛線性的，故而有的書上又稱雙線性形式為一次半線性形式。
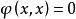雙線性形式
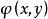雙線性形式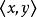 雙線性形式
雙線性形式條件(vi)實際上只是半正定性，因為並不能推出，有時候我們仿照內積的記號，記雙線性形式為。
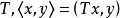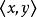雙線性形式 雙線性形式根據定義，對有界運算元是有界的雙線性形式，如果T還是自伴運算元或正運算元，則還是自伴或正定的。
相關定理
除了Hilbert空間上的有界線性運算元誘導的雙線性形式之外，還有沒有其他的雙線性形式?下面我們就來討論這個問題。
定理1
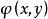雙線性形式如果是H上的有界雙線性形式，則存在唯一的有界運算元T，使
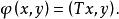雙線性形式推論
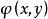雙線性形式如果是H上的有界共軛(正定)雙線性形式，則存在唯一的自伴(正)運算元T，使
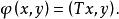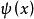雙線性形式
雙線性形式定義4 Hilbert空間H上的實函式如果滿足：
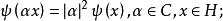雙線性形式(i)
雙線性形式(ii)
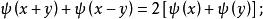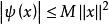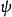雙線性形式
雙線性形式(iii) 存在M≥o，使，則稱為H上的 有界實二次形式。
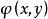雙線性形式
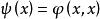雙線性形式由此可見，對有界的共軛雙線性形式，是H上的有界實二次形式，那么H上的任一有界實二次形式是否都是由某個共軛雙線性形式誘導的呢?下面的定理回答了這個問題。
定理2
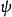雙線性形式 雙線性形式設是Hilbert空間H上的有界實二次形式，則存在唯一的有界共軛雙線性形式，使
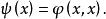雙線性形式推論
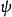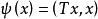雙線性形式
雙線性形式如果是H上有界實二次形式，則存在有界自伴運算元T，使。
定理3
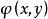雙線性形式如果是H上的正定雙線性形式，則有
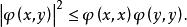雙線性形式特別地，如果T是正運算元，則有
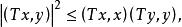雙線性形式上式稱為廣義Schwarz不等式。
