黎曼形式

黎曼形式是一種復正定雙線性形式。一個復環面的代數流形的充分必要條件為它容許一個黎曼形式。

簡介

黎曼形式是一種復正定雙線性形式。

設T為復環面，L為T的格（是由T的實基生成的）。設A:C ×C →R是實反對稱雙線性形式，若：

1、A(L,L)⊂Z；

2、A(ix,y)是C 上的對稱正定形式；

則稱A是T（或L）的黎曼形式。

一個復環面的代數流形的充分必要條件為它容許一個黎曼形式。

雙線性形式

設V是域F上的(n+1)維向量空間，如果函式σ：V×V→F，滿足條件：

σ(ax+bx,y)=aσ(x,y)+bσ(x,y)，a、b∈F，x、x、y∈V，

σ(x,ay+by)=aσ(x,y)+bσ(x,y)，a、b∈F，x、y、y∈V，

則σ稱為定義在V上的雙線性形式。

復環面

復環面是實環面的推廣。

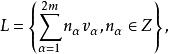黎曼形式

將復矢量空間C看做實2m維矢量空間R。在R中取2m個實線性無關的矢量{V}，它產生如下的格： 這裡Z表示整數群。C和L都是加群，商空間C/L成為一個m維的複流形，稱為m維復環面。