提出背景
實際遇到的常微分方程中,多數很難找到解析解。因此,學會用數值解法求出常微分方程的特解,即用表格或圖示法來表示近似滿足微分方程和初始條件的解。
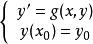 隱式歐拉法
隱式歐拉法思想:採用離散變數法,即把一個連續型問題轉化成一個離散型問題,即採用步進的方式求出方程在一些離散點上的近似值。
常微分方程初值問題的數值解法一般分為兩類,
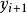 隱式歐拉法
隱式歐拉法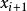 隱式歐拉法
隱式歐拉法 隱式歐拉法
隱式歐拉法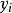 隱式歐拉法
隱式歐拉法(1)一步法,即在計算 時,只用計算 , 和 ,即前一步的值,其代表是歐拉法和龍格庫塔法
(2)多步法,還要用到前面n步的值,代表是亞當斯法
顯示歐拉方法
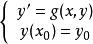 隱式歐拉法
隱式歐拉法 隱式歐拉法
隱式歐拉法推導過程: (1)消除導數項,用差商近似代替導數,將變數離散化。任取一點,設為 ,則有:
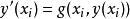 隱式歐拉法
隱式歐拉法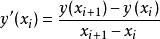 隱式歐拉法
隱式歐拉法(2)用(前項)差商公式 替代導數項,假設步長為h,得:
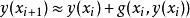 隱式歐拉法
隱式歐拉法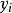 隱式歐拉法
隱式歐拉法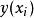 隱式歐拉法
隱式歐拉法(3)用 表示 得近似值,代入上式,得:
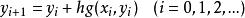 隱式歐拉法
隱式歐拉法註:精度是一階的
隱式歐拉法
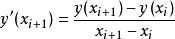 隱式歐拉法
隱式歐拉法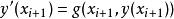 隱式歐拉法
隱式歐拉法顯示歐拉方法是用(前項)差商公式替代導數項,若採用向後差商 替代方程 中的導數項,再離散化,可導出:
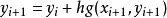 隱式歐拉法
隱式歐拉法註:精度是一階的
隱式改進歐拉法
對於隱式歐拉法,一般採用梯形公式來求解。
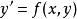 隱式歐拉法
隱式歐拉法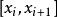 隱式歐拉法
隱式歐拉法對於方程 兩端在區間 上積分得:
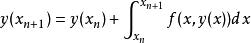 隱式歐拉法
隱式歐拉法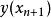 隱式歐拉法
隱式歐拉法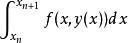 隱式歐拉法
隱式歐拉法要通過這個積分關係獲得 的近似值,只要近似地計算出其中的積分項
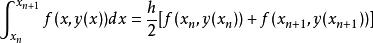 隱式歐拉法
隱式歐拉法再代入,得到
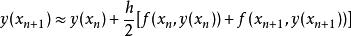 隱式歐拉法
隱式歐拉法這種差分格式稱為梯形格式。
比較
傳統的改進歐拉法是利用已知量,根據遞推公式逐次遞推計算出相應時段終點的函式值,因此是一種顯式解法。隱式改進歐拉法不是給出遞推公式,而是首先把微分方程化為差分方程,然後利用求解差分方程的方法確定函式值,其特點就是把微分方程的求解問題轉換成一系列代數方程的求解過程。
因此,隱式解法有兩個明顯的優點:一是當微分方程和代數方程需要聯立求解時,利用隱式解法便於消除交接誤差;二是隱式解法可以採取較大的步長。
