經典四階法
在各種龍格－庫塔法當中有一個方法十分常用，以至於經常被稱為“RK4”或者就是“龍格－庫塔法”。該方法主要是在已知方程導數和初值信息，利用計算機仿真時套用，省去求解微分方程的複雜過程。
令初值問題表述如下。
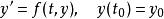龍格庫塔法則，對於該問題的RK4由如下方程給出：
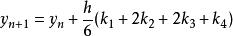龍格庫塔法其中
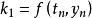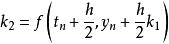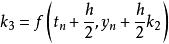龍格庫塔法
龍格庫塔法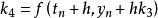
龍格庫塔法
龍格庫塔法這樣，下一個值（ y）由現在的值（ y）加上時間間隔（ h）和一個估算的斜率的乘積所決定。該斜率是以下斜率的加權平均：
•k是時間段開始時的斜率；
•k是時間段中點的斜率，通過歐拉法採用斜率k來決定y在點t+h/2的值；
•k也是中點的斜率，但是這次採用斜率k決定y值；
•k是時間段終點的斜率，其y值用k決定。
當四個斜率取平均時，中點的斜率有更大的權值：
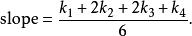龍格庫塔法RK4法是四階方法，也就是說每步的誤差是 h階，而總積累誤差為 h階。
注意上述公式對於標量或者向量函式（ y可以是向量）都適用。
顯式法
顯式龍格－庫塔法是上述RK4法的一個推廣。它由下式給出
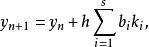龍格庫塔法其中
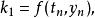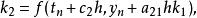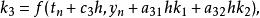龍格庫塔法
龍格庫塔法
龍格庫塔法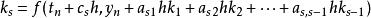
龍格庫塔法
龍格庫塔法（注意：上述方程在不同著述中有不同但卻等價的定義）。
要給定一個特定的方法，必須提供整數 s（級數），以及係數 a（對於1 ≤ j< i≤ s）, b（對於 i= 1, 2, ..., s）和 c（對於 i= 2, 3, ..., s）。
龍格庫塔法是自洽的，如果
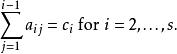龍格庫塔法如果要求方法的精度為 p階，即截斷誤差為O( h)的，則還有相應的條件。這些可以從截斷誤差本身的定義中導出。例如，一個2級2階方法要求 b+ b= 1, b c= 1/2, 以及 b a= 1/2。
例子
RK4法處於這個框架之內。其表為：
| 0 | ||||
| 1/2 | 1/2 | |||
| 1/2 | 0 | 1/2 | ||
| 1 | 0 | 0 | 1 | |
| 1/6 | 1/3 | 1/3 | 1/6 |
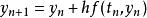龍格庫塔法然而，最簡單的龍格-庫塔法是（更早發現的）歐拉方法，其公式為。這是唯一自洽的一級顯式龍格庫塔方法。相應的表為：
| 0 | |
| 1 |
隱式方法
以上提及的顯式龍格庫塔法一般來講不適用於求解剛性方程。這是因為顯式龍格庫塔方法的穩定區域被局限在一個特定的區域裡。顯式龍格庫塔方法的這種缺陷使得人們開始研究隱式龍格庫塔方法，一般而言，隱式龍格庫塔方法具有以下形式：
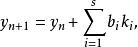龍格庫塔法
龍格庫塔法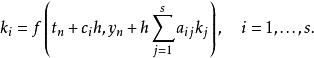其中
龍格庫塔法在顯式龍格庫塔方法的框架里，定義參數的矩陣是一個下三角矩陣，而隱式龍格庫塔方法並沒有這個性質，這是兩個方法最直觀的區別：
龍格庫塔法需要注意的是，與顯式龍格庫塔方法不同，隱式龍格庫塔方法在每一步的計算里需要求解一個線性方程組，這相應的增加了計算的成本。
程式
#include<stdio.h>
#include<math.h>
#define f(x,y) (-1*(x)*(y)*(y))
void main(void)
{
double a,b,x0,y0,k1,k2,k3,k4,h;
int n,i;
printf("input a,b,x0,y0,n:");
scanf("%lf%lf%lf%lf%d",&a,&b,&x0,&y0,&n);
printf("x0\ty0\tk1\tk2\tk3\tk4\n");
for(h=(b-a)/n,i=0;i!=n;i++)
{
k1=f(x0,y0);
k2=f(x0+h/2,y0+k1*h/2);
k3=f(x0+h/2,y0+k2*h/2);
k4=f(x0+h,y0+h*k3);
printf("%lf\t%lf\t",x0,y0);
printf("%lf\t%lf\t",k1,k2);
printf("%lf\t%lf\n",k3,k4);
y0+=h*(k1+2*k2+2*k3+k4)/6;
x0+=h;
}
printf("xn=%lf\tyn=%lf\n",x0,y0);
}
運行結果：
input a,b,x0,y0,n:0 5 0 2 20
x0 y0 k1 k2 k3 k4
0.000000 2.000000 -0.000000 -0.500000 -0.469238
-0.886131
0.250000 1.882308 -0.885771 -1.176945 -1.129082
-1.280060
0.500000 1.599896 -1.279834 -1.295851 -1.292250
-1.222728
0.750000 1.279948 -1.228700 -1.110102 -1.139515
-0.990162
1.000000 1.000027 -1.000054 -0.861368 -0.895837
-0.752852
1.250000 0.780556 -0.761584 -0.645858 -0.673410
-0.562189
1.500000 0.615459 -0.568185 -0.481668 -0.500993
-0.420537
1.750000 0.492374 -0.424257 -0.361915 -0.374868
-0.317855
2.000000 0.400054 -0.320087 -0.275466 -0.284067
-0.243598
2.250000 0.329940 -0.244935 -0.212786 -0.218538
-0.189482
2.500000 0.275895 -0.190295 -0.166841 -0.170744
-0.149563
2.750000 0.233602 -0.150068 -0.132704 -0.135399
-0.119703
3.000000 0.200020 -0.120024 -0.106973 -0.108868
-0.097048
3.250000 0.172989 -0.097256 -0.087300 -0.088657
-0.079618
3.500000 0.150956 -0.079757 -0.072054 -0.073042
-0.066030
3.750000 0.132790 -0.066124 -0.060087 -0.060818
-0.055305
4.000000 0.117655 -0.055371 -0.050580 -0.051129
-0.046743
4.250000 0.104924 -0.046789 -0.042945 -0.043363
-0.039833
4.500000 0.094123 -0.039866 -0.036750 -0.037072
-0.034202
4.750000 0.084885 -0.034226 -0.031675 -0.031926
-0.029571
xn=5.000000 yn=0.076927
