簡介
隨機並行梯度下降算法（stochastic parallel gradient descent algorithm），簡稱SPGD算法。作為一種無模型最佳化算法，比較適用於控制變數較多，受控系統比較複雜，無法建立準確數學模型的最最佳化控制過程。
發展歷程
SPGD控制算法原理主要發展於隨機逼近（Stochastic Approximation，簡稱 SA）理論和人工神經網路（Artificial Neural Networks）技術，美國陸軍研究實驗室的Voronstov在同時擾動隨機近似控制算法基礎上開發的自適應光學校正技術。
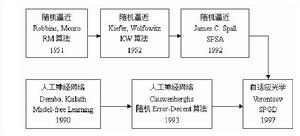隨機並行梯度下降算法發展歷程套用背景
由於星地鏈路之間的主要傳輸介質是大氣，穿過路徑較長，大氣分子對於雷射光束的吸收與散射將引起傳播方向上光能的衰減，因此傳輸信道中的大氣湍流是限制通信距離及通信系統性能的瓶頸之一，不僅需要考慮大氣對雷射的吸收與散射，還必須考慮大氣的湍流效應。大氣湍流會使光載波在傳輸過程中隨機地改變其光束特性，致使攜帶信息的光波的強度和相位在空間和時間上都呈現隨機起伏，造成閃爍現象，極大地降低了系統的成像質量或光束質量。基於隨機並行下降算法的自適應光學技術可以提高雷射作用到目標上的聚集程度；降低空間目標在望遠鏡成像面上的模糊程度，提高目標識別的準確度，實現對目標的精跟蹤；提高雷射通信系統的載波光束質量，降低系統的噪聲水平、提高數據傳輸速率等，在天文自適應成像領域已得到成功套用。
無需波前感測器的像清晰化技術在不需要波前感測器的條件下，以成像清晰度和接受光能量為性能指標直接作為算法最佳化的目標函式，最佳化得到接近理想的校正效果，系統複雜性大大降低，比較適合用於補償大氣湍流帶來的閃爍現象。
相對其他算法的優勢
第一：由於不需要進行波前測量，系統中不需要採用波前感測器，也無需進行波前重構，而是以成像清晰度和接受光能量為性能指標直接作為算法最佳化的目標函式，降低了系統和算法的複雜性。
第二：所有驅動單元控制信號並行計算，使得未來極高解析度的波前校正成為可能。對於傳統的波前感測技術來說，高解析度的波前校正其波前重構的計算量也是相當巨大的。此時，像清晰化自適應光學系統由於校正算法簡單，對這樣的波前校正器件則具有更好的適應性。
第三：由於無需波前重構，大氣湍流帶來的閃爍不影響算法的疊代以及反饋裝置的數據採集，在大氣湍流較強或光束長程傳輸套用中有其獨特優勢。
算法流程
第一步，測量系統當前的像質評價函式值；
第二步，對控制參量 施加擾動 ，隨機生成擾動向量，各擾動向量相互獨立且同為伯努利分布；
第三步，保持控制參量的擾動狀態，測量此時系統的像質評價函式值；
第四步，計算像質評價函式值的改變數，並按疊代公式對控制參量的取值進行修正；下圖為隨機並行梯度下降算法的疊代公式。
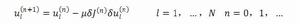隨機並行梯度下降算法疊代公式
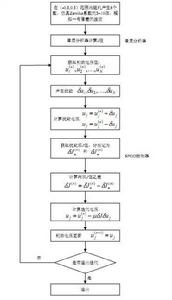隨機並行梯度下降算法流程圖