起源發展
進化計算包括遺傳算法(Genetic Algorithms)、遺傳規劃(Genetic Programming)、進化策略(Evolution Strategies)和進化規劃(Evolution Programming)4種典型方法。第一類方法比較成熟,現已廣泛套用,進化策略和進化規劃在科研和實際問題中的套用也越來越廣泛。
遺傳算法的主要基因操作是選種、交配和突變,而在進化規則、進化策略中,進化機制源於選種和突變。就適應度的角度來說遺傳算法用於選擇優秀的父代(優秀的父代產生優秀的子代),而進化規則和進化策略則用於選擇子代(優秀的子代才能存在)。遺傳算法與遺傳規劃強調的是父代對子代的遺傳鏈,而進化規則和進化策略則著重於子代本身的行為特性,即行為鏈。進化規則和進化策略一般都不採用編碼,省去了運作過程中的編碼—解碼手續更適用於連續最佳化問題,但因此也不能進行非數值最佳化。進化策略可以確定機制產生出用於繁殖的父代,而遺傳算法和進化規則強調對個體適應度和機率的依賴。
此外,進化規則把編碼結構抽象為種群之間的相似,而進化策略抽象為個體之間的相似。進化策略和進化規則已套用於連續函式最佳化、模式識別、機器學習、神經網路訓練、系統辨識和智慧型控制的眾多領域。
從本世紀40年代起,生物模擬就構成了計算科學的一個組成部分,象早期的自動機理論,就是假設機器是由類似於神經元的基本元素組成的,它向人們展示了第一個自複製機模型。這些年來諸如機器能否思維、基於規則的專家系統是否能勝任人類的工作,以及神經網路可否使機器具有看和聽的功能等有關生物類比的問題已成為人工智慧關注的焦點。最近生物計算在機器昆蟲和種群動態系統模擬上所取得的成功激勵越來越多的人們致力於人工生命領域的研究。當今計算機科學家和分子生物學家已開始攜手進行合作研究,並且類比也得到了更為廣泛的套用。
自然界生物體通過自身的演化就能使問題得到完美的解決。這種能力讓最好的電腦程式也相形見拙。計算機科學家為了某個算法可能要耗費數月甚至幾年的努力,而生物體通過進化和自然選擇這種非定向機制就達到了這個目的。
近三十年的不斷的研究和套用已經清楚地表明了模擬自然進化的搜尋過程可以產生非常魯棒(robust)的計算機算法,雖然這些模型還只是自然界生物體的粗糙簡化。進化算法就是基於這種思想發展起來的一類隨機搜尋技術,它們是模擬由個體組成的群體的集體學習過程。其中每個個體表示給定問題搜尋空間中的一點。進化算法從任一初始的群體出發,通過隨機選擇(在某些算法中是確定的)、變異和重組(在某些算法中被完全省去)過程,使群體進化到搜尋空間中越來越好的區域。選擇過程使群體中適應性好的個體比適應性差的個體有更多的複製機會,重組運算元將父輩信息結合在一起並將他們傳到子代個體,變異在群體中引人了新的變種。
目前研究的進化算法主要有三種典型的算法:遺傳算法、進化規劃和進化策略。這三種算法是彼此獨立發展起來的,遺傳算法由美國J.Holand創建,後由K.De Jong,J.Grefenstette,D.Goldberg和L.navis等人進行了改進;進化規劃最早由美國的L·J·Fogel,A.J.Owens和M.J.walsh提出,最近又由D.B.Fogel進行了完善;進化策略是由德國的I·Reehenberg和H.p.Sehwefel建立的。
群體搜尋策略和群體中個體之間的信息交換是進化算法的兩大特點。它們的優越性主要表現在:首先,進化算法在搜尋過程中不容易陷入局部最優,即使在所定義的適應度函式是不連續的,非規則的或有噪聲的情況下,它們也能以很大的機率找到全局最優解;其次,由於它們固有的並行性,進化算法非常適合於巨量並行機;再者,進化算法採用自然進化機制來表現複雜的現象,能夠快速可靠地解決非常困難的問題;此外,由於它們容易介人到已有的模型中並且具有可擴展性,以及易於同別的技術混和等因素,進化算法目前已經在最最佳化、機器學習和並行處理等領域得到了越來越廣泛的套用。1993年德國Dortmound大學的等人在一份研究t報告中蒐集了篇有關進化算法的套用的科技文獻。
簡介
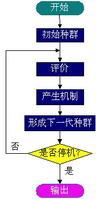 進化算法
進化算法進化算法包括遺傳算法、遺傳規劃、進化規劃和進化策略等等。進化算法的基本框架還是簡單遺傳算法所描述的框架,但在進化的方式上有較大的差異,選擇、交叉、變異、種群控制等有很多變化,進化算法的大致框圖可描述如右圖所示:
同遺傳算法一樣,進化算法的收斂性也有一些結果,文獻證明了在保存最優個體時通用的進化計算是收斂的,但進化算法的很多結果是從遺傳算法推過去的。
遺傳算法對交叉操作要看重一些,認為變異操作是算法的輔助操作;而進化規劃和進化策略認為在一般意義上說交叉並不優於變異,甚至可以不要交叉操作。
進化計算是基於自然選擇和自然遺傳等生物進化機制的一種搜尋算法。與普通的搜尋方法一樣,進化計算也是一種疊代算法,不同的是進化計算在最優解的搜尋過程中,一般是從原問題的一組解出發改進到另一組較好的解,再從這組改進的解出發進一步改進。而且在進化問題中,要求當原問題的最佳化模型建立後,還必須對原問題的解進行編碼。進化計算在搜尋過程中利用結構化和隨機性的信息,使最滿足目標的決策獲得最大的生存可能,是一種機率型的算法。
一般來說,進化計算的求解包括以下幾個步驟:給定一組初始解;評價當前這組解的性能;從當前這組解中選擇一定數量的解作為疊代後的解的基礎;再對其進行操作,得到疊代後的解;若這些解滿足要求則停止,否則將這些疊代得到的解作為當前解重新操作。
以遺傳算法為例,其工作步驟可概括為:
(1) 對工作對象——字元串用二進制的0/1或其它進制字元編碼。
(2) 根據字元串的長度L,隨即產生L個字元組成初始個體。
(3) 計算適應度。適應度是衡量個體優劣的標誌,通常是所研究問題的目標函式。
(4) 通過複製,將優良個體插入下一代新群體中,體現“優勝劣汰”的原則。
(5) 交換字元,產生新個體。交換點的位置是隨機決定的
(6) 對某個字元進行補運算,將字元1變為0,或將0變為1,這是產生新個體的另一種方法,突變字元的位置也是隨機決定的。
(7) 遺傳算法是一個反覆疊代的過程,每次疊代期間,要執行適應度計算、複製、交換、突變等操作,直至滿足終止條件。
將其用形式化語言表達,則為:假設α∈I記為個體,I記為個體空間。適應度函式記為Φ:I→R。在第t代,群體P(t)={a1(t),a2(t),…,an(t)}經過複製r(reproduction)、交換c(crossover)及突變m(mutation)轉換成下一代群體。這裡r、c、m均指宏運算元,把舊群體變換為新群體。L:I→{True, Flase}記為終止準則。利用上述符號,遺傳算法可描述為:
框架
進化算法是以達爾文的進化論思想為基礎,通過模擬生物進化過程與機制的求解問題的自組織、自適應的人工智慧技術。生物進化是通過繁殖、變異、競爭和選擇實現的;而進化算法則主要通過選擇、重組和變異這三種操作實現最佳化問題的求解。如下
其中r、m、s分別表示重組運算元、變異運算元、選擇運算元。圖1:進化算法基本框架
特點
進化計算是一種具有魯棒性的方法,能適應不同的環境不同的問題,而且在大多數情況下都能得到比較滿意的有效解。他對問題的整個參數空間給出一種編碼方案,而不是直接對問題的具體參數進行處理,不是從某個單一的初始點開始搜尋,而是從一組初始點搜尋。搜尋中用到的是目標函式值的信息,可以不必用到目標函式的導數信息或與具體問題有關的特殊知識。因而進化算法具有廣泛的套用性,高度的非線性,易修改性和可並行性。
此外,算法本身也可以採用動態自適應技術,在進化過程中自動調整算法控制參數和編碼精度,比如使用模糊自適應法。
進化策略
進化策略(ES)是在1965年由Rechenberg和Schwefel獨立提出的。
進化策略的一般算法
(1) 問題為尋找實值n維矢量x,使得函式F(x): R→R取極值。不失一般性,設此程式為極小化過程。
(2) 從各維的可行範圍內隨機選取親本 xi,i = 1, … , p的始值。初始試驗的分布一般是均勻分布。
(3) 通過對於x的每個分量增加零均值和預先選定的標準差的高斯隨機變數,從每個親本 xi產生子代 xi’。
(4) 通過將適應度F( xi)和F( xi’),i=1,…,P進行排序,選擇並決定那些矢量保留。具有最小適應度的P個矢量變成下一代的新親本。
進行新試驗,選擇具有最小方差的新子代,一直到獲得充分解,或者直到滿足某個終止條件。
在這個模型中,把試驗解的分量看做個體的行為特性,而不是沿染色體排列的基因。假設不管發生什麼遺傳變換,所造成各個個體行為的變化均遵循零均值和某個標準差的高斯分布。
由於基因多效性和多基因性,特定基因的改變可以影響許多表現型特徵。所以在創造新子系時,較為合適的是同時改變親本所有分量。
(1+1) — ES :
早期的進化策略的種群中只包含一個個體,並且只使用變異操作。在每一代中,變異後的個體與其父代進行比較,並選擇較好的一個,這種選擇策略被稱為(1+1)策略。
(1+1)—ES的缺點:
(1) 各維取定常的標推差使得程式收斂到最優解的速度很慢;
(2) 點到點搜尋的脆弱本質使得程式在局部極值附近容易受停滯的影響(雖然此算法表明可以漸近地收斂到全局最優點)。
( μ+λ ) — ES:μ個親本製造λ個子代,所有解均參加生存競爭,選出最好的μ個作為下一代的親本。
( μ,λ ) — ES:只有λ個子代參加生存競爭,在每代中μ個親本被完全取代。
1 .個體的表示法:
每個解矢量不僅包括了n維試驗矢量 x,而且還包括了擾動矢量σ,後者給出如何變異 x以及它本身如何變異的指令。
2 .變異:
設 x為當前矢量。σ為對應於 x每個維的方差矢量,於是新的解矢量 x’, σ’可以這樣產生:
3 .交叉:
4 .選擇
在進化策略中,選擇是按完全確定的方式進行。(μ,λ)—ES是從λ個子代個體集中選擇μ(1<μ<λA=個最好的個體;(μ+λ)—ES是從父代和子代個體的並集中選擇μ個最好的個體。雖然(μ+λ)—ES保留最優的個體能保證性能單調提高,但這種策略不能處理變化的環境,因此,目前選用最多的還是(μ,λ)—ES。
進化規劃
進化規劃(EP)由Fogel在20世紀60年代提出。
1 .表示法和適應值度量
進化規劃假設—個有界子空間 ,其中 ui< vi。搜尋區域被擴展到I=R,即個體為目標變數向量, a = x ∈ I,進化規劃把目標函式值通過比例變換到正值,同時加入某個隨機改變 θ來得到適應值 ,其中δ是比例函式。
2 .變異
可簡化為:
3 .選擇
在P個父代個體每個經過一次變異產生P個子代後,進化規劃利用一種隨機q競爭選擇方法從父代和子代的集合中選擇P個個體,其中q>1是選擇算法的參數。
差分算法
差分進化算法(Differential Evolution, DE)是一種新興的進化計算技術,或稱為差分演化算法、微分進化算法、微分演化算法、差異演化算法。它是由Storn等人於1995年提出的,最初的構想是用於解決切比雪夫多項式問題,後來發現DE也是解決複雜最佳化問題的有效技術。DE與人工生命,特別是進化算法有著極為特殊的聯繫。
差分進化算法是基於群體智慧型理論的最佳化算法,通過群體內個體間的合作與競爭產生的群體智慧型指導最佳化搜尋。但相比於進化算法,DE保留了基於種群的全局搜尋策略,採用實數編碼基於差分的簡單變異操作和一對一的競爭生存策略,降低了遺傳操作的複雜性。同時,DE特有的記憶能力使其可以動態跟蹤當前的搜尋情況,以調整其搜尋策略,具有較強的全局收斂能力和魯棒性,且不需要藉助問題的特徵信息,適於求解一些利用常規的數學規劃方法所無法求解的複雜環境中的最佳化問題。
差分進化算法是一種基於群體進化的算法,具有記憶個體最優解和種群內信息共享的特點,即通過種群內個體間的合作與競爭來實現對最佳化問題的求解,其本質是一種基於實數編碼的具有保優思想的貪婪遺傳算法。
DE是一種用於最佳化問題的啟發式算法。本質上說,它是一種基於實數編碼的具有保優思想的貪婪遺傳算法 。同遺傳算法一樣,DE包含變異和交叉操作,但同時相較於遺傳算法的選擇操作,DE採用一對一的淘汰機制來更新種群。由於DE在連續域最佳化問題的優勢已獲得廣泛套用,並引發進化算法研究領域的熱潮。
DE由Storn 以及Price提出,算法的原理採用對個體進行方向擾動,以達到對個體的函式值進行下降的目的,同其他進化算法一樣,DE不利用目標函式的梯度信息,因此對目標的可導性甚至連續性沒有要求,適用性很強。同時,算法與粒子群最佳化有相通之處,但因為DE在一定程度上考慮了多變數間的相關性,因此相較於粒子群最佳化在變數耦合問題上有很大的優勢。算法的實現參考實現代碼部分。

