簡介
受限玻爾茲曼機是玻爾茲曼機(Boltzman machine,BM)的一種特殊拓撲結構。BM的原理起源於統計物理學,是一種基於能量函式的建模方法,能夠描述變數之間的高階相互作用,BM的學習算法較複雜,但所建模型和學習算法有比較完備的物理解釋和嚴格的數理統計理論作基礎。BM是一種對稱耦合的隨機反饋型二值單元神經網路,由可見層和多個隱層組成,網路節點分為可見單元(visible unit)和隱單元(hidden unit),用可見單元和隱單元來表達隨機網路與隨機環境的學習模型,通過權值表達單元之間的相關性。
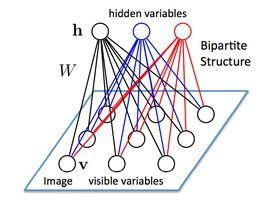
正如名字所提示的那樣,受限玻茲曼機是一種玻茲曼機的變體,但限定模型必須為二分圖。模型中包含對應輸入參數的輸入(可見)單元和對應訓練結果的隱單元,圖中的每條邊必須連線一個可見單元和一個隱單元。(與此相對,“無限制”玻茲曼機包含隱單元間的邊,使之成為遞歸神經網路。)這一限定使得相比一般玻茲曼機更高效的訓練算法成為可能,特別是基於梯度的對比分歧(contrastive divergence)算法。
受限玻茲曼機也可被用於深度學習網路。具體地,深度信念網路可使用多個RBM堆疊而成,並可使用梯度下降法和反向傳播算法進行調優。
以Hinton和Ackley兩位學者為代表的研究人員從不同領域以不同動機同時提出BM學習機。
Smolensky提出的RBM由一個可見神經元層和一個隱神經元層組成,由於隱層神經元之間沒有相互連線並且隱層神經元獨立於給定的訓練樣本,這使直接計算依賴數據的期望值變得容易,可見層神經元之間也沒有相互連線,通過從訓練樣本得到的隱層神經元狀態上執行馬爾可夫鏈抽樣過程,來估計獨立於數據的期望值,並行交替更新所有可見層神經元和隱層神經元的值。
BM是由Hinton和Sejnowski提出的一種隨機遞歸神經網路,可以看做是一種隨機生成的Hopfield網路,是能夠通過學習數據的固有內在表示解決困難學習問題的最早的人工神經網路之一,因樣本分布遵循玻爾茲曼分布而命名為BM。BM由二值神經元構成,每個神經元只取1或0這兩種狀態,狀態1代表該神經元處於接通狀態,狀態0代表該神經元處於斷開狀態。在下面的討論中單元和節點的意思相同,均表示神經元。
結構
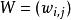 受限玻爾茲曼機
受限玻爾茲曼機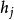 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機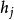 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機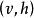 受限玻爾茲曼機
受限玻爾茲曼機標準的受限玻爾茲曼機由二值(布爾/伯努利)隱層和可見層單元組成。權重矩陣 中的每個元素指定了隱層單元 和可見層單元 之間邊的權重。此外對於每個可見層單元 有偏置 ,對每個隱層單元 有偏置 以及在這些定義下,一種受限玻爾茲曼機配置(即給定每個單元取值)的“能量”被定義為
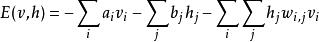 受限玻爾茲曼機
受限玻爾茲曼機或者用矩陣的形式表示如下:
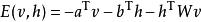 受限玻爾茲曼機
受限玻爾茲曼機這一能量函式的形式與霍普菲爾德神經網路相似。在一般的玻爾茲曼機中,隱層和可見層之間的聯合機率分布由能量函式給出:
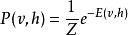 受限玻爾茲曼機
受限玻爾茲曼機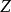 受限玻爾茲曼機
受限玻爾茲曼機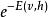 受限玻爾茲曼機
受限玻爾茲曼機其中, 為配分函式,定義為在節點的所有可能取值下 的和(亦即使得機率分布和為1的歸一化常數)。類似地,可見層取值的邊緣分布可通過對所有隱層配置求和得到:
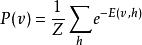 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機由於RBM為一個二分圖,層內沒有邊相連,因而隱層是否激活在給定可見層節點取值的情況下是條件獨立的。類似地,可見層節點的激活狀態在給定隱層取值的情況下也條件獨立。亦即,對 個可見層節點和 個隱層節點,可見層的配置v對於隱層配置h的條件機率如下:
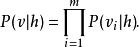 受限玻爾茲曼機
受限玻爾茲曼機類似地,h對於v的條件機率為
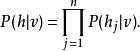 受限玻爾茲曼機
受限玻爾茲曼機其中,單個節點的激活機率為
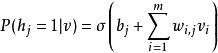 受限玻爾茲曼機
受限玻爾茲曼機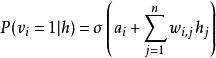 受限玻爾茲曼機
受限玻爾茲曼機和
 受限玻爾茲曼機
受限玻爾茲曼機其中 代表邏輯函式。
訓練算法
 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機受限玻爾茲曼機的訓練目標是針對某一訓練集,最大化機率的乘積。其中,被視為一矩陣,每個行向量作為一個可見單元向量:
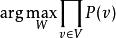 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機或者,等價地,最大化的對數機率期望:
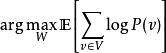 受限玻爾茲曼機
受限玻爾茲曼機 受限玻爾茲曼機
受限玻爾茲曼機訓練受限玻爾茲曼機,即最最佳化權重矩陣,最常用的算法是傑弗里·辛頓提出的對比分歧(contrastive divergence,CD)算法。這一算法最早被用於訓練辛頓提出的“專家積”模型。這一算法在梯度下降的過程中使用吉布斯採樣完成對權重的更新,與訓練前饋神經網路中利用反向傳播算法類似。
基本的針對一個樣本的單步對比分歧(CD-1)步驟可被總結如下:
取一個訓練樣本v,計算隱層節點的機率,在此基礎上從這一機率分布中獲取一個隱層節點激活向量的樣本h;
計算v和h的外積,稱為“正梯度”;
從h獲取一個重構的可見層節點的激活向量樣本v',此後從v'再次獲得一個隱層節點的激活向量樣本h';
計算v'和h'的外積,稱為“負梯度”;
1.取一個訓練樣本v,計算隱層節點的機率,在此基礎上從這一機率分布中獲取一個隱層節點激活向量的樣本h;
2.計算v和h的外積,稱為“正梯度”;
3.從h獲取一個重構的可見層節點的激活向量樣本v',此後從v'再次獲得一個隱層節點的激活向量樣本h';
4.計算v'和h'的外積,稱為“負梯度”;
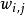 受限玻爾茲曼機
受限玻爾茲曼機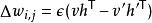 受限玻爾茲曼機
受限玻爾茲曼機使用正梯度和負梯度的差以一定的學習率更新權重:。
偏置a和b也可以使用類似的方法更新。
功能
深信任網路(deep belief network,DBN)和深玻爾茲曼機(deep Boltzmann machine,DBM),由多層神經元組成,已經套用於許多機器學習任務中,能夠很好地解決一些複雜問題,在一定程度上提高了學習性能。深神經網路由許多受限玻爾茲曼機(restricted Boltzmann machine,RBM)堆疊構成,RBM的可見層神經元之間和隱層神經元之間假定無連線。深神經網路用層次無監督貪婪預訓練方法分層預訓練RBM,將得到的結果作為監督學習訓練機率模型的初始值,學習性能得到很大改善。無監督特徵學習就是將RBM的複雜層次結構與大量數據集之間實現統計建模。通過無監督預訓練使網路獲得高階抽象特徵,並且提供較好的初始權值,將權值限定在對全局訓練有利的範圍內,使用層與層之間的局部信息進行逐層訓練,注重訓練數據自身的特性,能夠減小對學習目標過擬合的風險,並避免深神經網路中誤差累積傳遞過長的問題。RBM由於表示力強、易於推理等優點被成功用作深神經網路的結構單元使用,在近些年受到廣泛關注,作為實際套用,RBM的學習算法已經在MNIST和NORB等數據集上顯示出優越的學習性能。RBM的學習在深度神經網路的學習中占據核心的地位。
套用
BM及其模型已經成功套用於協同濾波、分類、降維、圖像檢索、信息檢索、語言處理、自動語音識別、時間序列建模、文檔分類、非線性嵌入學習、暫態數據模型學習和信號與信息處理等任務。受限玻爾茲曼機在降維、分類、協同過濾、特徵學習和主題建模中得到了套用。根據任務的不同,受限玻爾茲曼機可以使用監督學習或無監督學習的方法進行訓練。