由來及意義
廣義坐標的概念由Lagrange(拉格朗日)提出,在拉格朗日之前人們已經用它解決過一些問題。
例如:Eular(歐拉)描述剛體運動的三獨立變數——歐拉角
廣義坐標的提出雖然只是描述方法上的改進,但是對力學發展產生了深遠影響。
廣義坐標不僅擺脫了卡氏坐標下的多體系統研究中約束所造成的巨大困難,並用最少的參數描述系統位形。同時,由於坐標的相互獨立性,研究系統運動也有利得多。
獨立廣義坐標
當分析有的問題時(尤其是當有許多約束條件的時候),儘量選擇獨立的廣義坐標。因為,這樣可以減少代表約束的變數。但是,當遇到非完整約束時,或者當計算約束力時,就必須使用關於這約束力的,相依的廣義坐標。
 廣義坐標
廣義坐標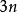 廣義坐標
廣義坐標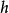 廣義坐標
廣義坐標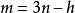 廣義坐標
廣義坐標 廣義坐標
廣義坐標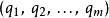 廣義坐標
廣義坐標 廣義坐標
廣義坐標在三維空間裡,假設一個物理系統擁有顆粒子;那么,這系統的自由度是。再假設這系統有個完整約束;那么,這系統的自由度變為。必須用個獨立廣義坐標與時間來完全描述這系統的運動。坐標的轉換方程可以表示如下:
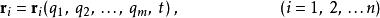 廣義坐標
廣義坐標雖然我們可能會遇到複雜的系統時,這轉換方程具有足夠的靈活性來選擇最合適的坐標。在思考虛位移與廣義力時,這轉換方程也可以用來建造微分。
理論說明
對於含有n個質點的質點系,在空間有3n個坐標。若這些質點間存在k個有限約束,則約束方程可寫為:fs(xx…,xt)=0(s=1,2,…,k)。利用約束方程消去3n個坐標中的k個變數,剩下N=3n-k個變數是獨立的。利用變數轉換,可將這N個變數用其他任何N個獨立變數qq…,q來表示。因此,n個x坐標可用N個q表示為x=x(qq…,qt)(i=1,2…,3n)。這種相互獨立的變數稱為廣義坐標,其數目N等於完整系統的自由度。
常用的廣義坐標有線量和角量兩種。例如,對約束在空間固定曲線上運動的質點,可用自始點計量的路程s作廣義坐標;用細桿約束在豎直平面內擺動的質點,可用桿與鉛垂線的夾角θ作廣義坐標。廣義坐標對時間的導數稱廣義速度。同樣,因為問題需要也會有廣義加速度、廣義動量、廣義角動量等。
例子
 廣義坐標
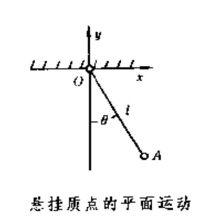
廣義坐標例如以長為l的細繩,懸掛一質點A於固定點O,使它在Oxy平面內運動(見圖)。質點坐標為(x,y),即n=2,它與一個約束方程x +y =l 相聯繫,故N=n-1=1,只有一個廣義坐標。按問題的性質,選用繩與鉛垂線的夾角θ為廣義坐標。這樣,便有 :
x=lsinθ,y=-lcosθ。

