閔科夫斯基，H.
正文
德國數學家。在數論與代數領域作出了重大貢獻，為狹義相對論奠定了數學基礎。1864年 6月22日生於立陶宛，1909年1月12日卒于格丁根。父母是德國人。8歲時全家定居柯尼斯堡（現蘇聯加里寧格勒）。在柯尼斯堡大學學習期間，與D.希爾伯特及A.胡爾維茨結為終身摯友。1892年任波恩大學副教授，1894年接替希爾伯特任柯尼斯堡大學教授，1896年到蘇黎世執教，1902年起任哥廷根大學教授。 1881年，巴黎科學院宣布1883年大獎的主題是一個整數分解為五個平方數之和的表示法的數目。英國數學家H.J.S.史密斯在1859年已得到該問題的答案。18歲的閔科夫斯基在長達140頁的論文中建立了n個變數的整係數二次型的理論體系，對二次型的“屬”提出了更一般、更自然的定義，因而獨立地得到了更好的公式。後與史密斯同時獲獎。此後他經常研究的一個主題是 n個變數的二次型。他通過三個不變數刻畫了有理係數二次型在有理係數線性變換下的等價性，完成了實係數正定二次型的約化理論，提供了在每個類中只給出惟一的約化形式的約化過程。為了簡化P.G.L.狄利克雷和C.埃爾米特建立的丟番圖逼近的解析理論，他把格和凸集等幾何概念引入數論，他稱由這一簡單而又有效的方法所建立的理論為“數的幾何”。“丟番圖逼近”一詞就是他首創的。利用這種幾何方法，他推動了連分數理論的發展，給出了判定一個數是否為代數數的算法。他在n 維空間中定義了支撐超平面和支撐函式的概念，證明了凸體在其任一邊界點處存在支撐超平面。他看出通過n 維空間中的對稱凸體可以定義一種新的“距離”概念，因而就能產生相應的“幾何”。這一想法為建立線性賦范空間（見巴拿赫空間）概念鋪平了道路。他還引進了幾個凸體的“混合體積”的概念，發現了有關的基本關係式。
閔科夫斯基對數學物理很有興趣。1905年，他同希爾伯特決定在他們主持的討論班上研究運動物體的電動力學。他通過
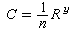(с為光速)為狹義相對論提供了四維時空數學結構，被稱為“閔科夫斯基世界”。諾貝爾物理學獎金得獎人M.玻恩曾說，他在閔科夫斯基的工作中找到了"相對論數學的整個武庫"。 閔科夫斯基的主要論著有:《數的幾何》(1896),《算術等價的不連續性》（1905），《丟番圖逼近》(1907)，《時間與空間》(1907)，《兩篇關於電動力學基本公式的論文》(1909)等。
