公式簡介
閔可夫斯基（Hermann Minkowski，1864－1909）出生於俄國的 Alexotas (現在變成立陶宛的 Kaunas)。父親是一個成功的猶太商人，但是當時的俄國政府迫害猶太人，所以當閔可夫斯基八歲時，父親就帶全家搬到普魯士的 Konigsberg (哥尼斯堡)定居，和另一位數學家希爾伯特（Hilbert ）的家僅一河之隔。閔可夫斯基有兩個哥哥，他是么弟。大哥 Max 在俄國時因為種族歧視，不能進學校讀書，後來也一直沒有受正規教育，長大後與他父親一起經商，繼承父業成為一個成功的商人。二哥就是發現胰島素和糖尿病關聯的著名醫學家 Oscar Minkowski，人稱“胰島素之父”。閔可夫斯基本人則因數學才能出眾，早有神童之名，後來更是優秀的數學家。他們兄弟三人都十分傑出，在Konigsberg曾經轟動一時。
閔可夫斯基的主要工作在數論、代數和數學物理上。在數論上，他對二次型進行了重要的研究。在1881年法國大獎中，Minkowski深入鑽研了高斯（Gauss）、狄利克雷（Dirichlet） 等人的論著。因為Gauss曾在研究把一個整數分解為三個平方數之和時用了二元二次型的性質，Minkowski由前人的工作中認識到把一個整數分解為五個平方數之和的方法與四元二次型有關。由此，他深入研究了n元二次型，建立了完整的理論體系。這樣一來，原題就很容易從更一般的理論中得出，Minkowski交給法國科學院的論文長達140頁，遠遠超出了原題的範圍。
定義
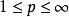閔可夫斯基不等式
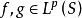閔可夫斯基不等式
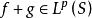閔可夫斯基不等式設 S是一個度量空間， ， ，那么 ，我們有：
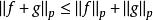閔可夫斯基不等式
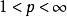閔可夫斯基不等式
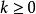閔可夫斯基不等式
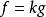閔可夫斯基不等式
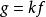閔可夫斯基不等式如果 ，等號成立若且唯若 ， 或
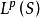閔可夫斯基不等式閔可夫斯基不等式是 中的三角不等式。它可以用赫爾德不等式來證明。和赫爾德不等式一樣，閔可夫斯基不等式取可數測度可以寫成序列或向量的特殊形式：
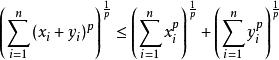閔可夫斯基不等式
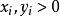閔可夫斯基不等式
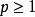閔可夫斯基不等式
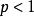閔可夫斯基不等式其中 ，且 ；若 ，則不等式的≤變為≥ 。
證明
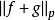閔可夫斯基不等式我們考慮 的 p次冪：
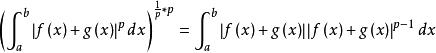閔可夫斯基不等式
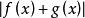閔可夫斯基不等式（用三角形不等式展開 ）
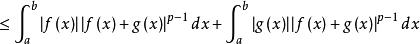閔可夫斯基不等式（用赫爾德不等式）
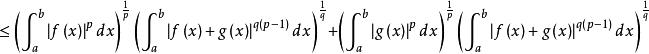閔可夫斯基不等式
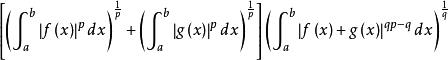閔可夫斯基不等式=
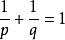閔可夫斯基不等式（利用 p= qp−q，因為 ）
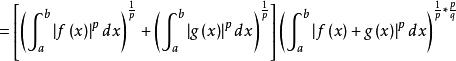閔可夫斯基不等式現在我們考慮這個不等式序列的首尾兩項，除以最後那個表達式的後面那個因子，我們得到:
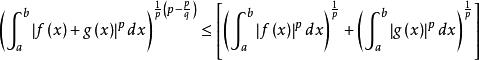閔可夫斯基不等式
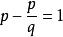閔可夫斯基不等式因為 ，我們最終得出：
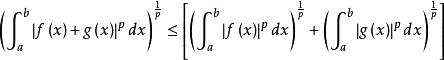閔可夫斯基不等式這就是我們所要的結論。
對於序列的情況，證明是完全類似的。
一般形式
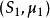閔可夫斯基不等式
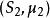閔可夫斯基不等式
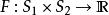閔可夫斯基不等式假設 和 是兩個測度空間， 是積空間上的可測函式，則
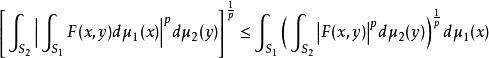閔可夫斯基不等式
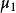閔可夫斯基不等式
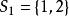閔可夫斯基不等式
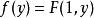閔可夫斯基不等式
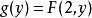閔可夫斯基不等式當 是 上的計數測度時，令 ， ，一般形式即為
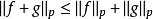閔可夫斯基不等式統計學形式
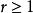閔可夫斯基不等式對於任意 ，只要隨機變數X和Y有r階絕對矩，則：
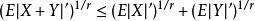閔可夫斯基不等式
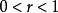閔可夫斯基不等式當 時，有：
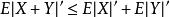閔可夫斯基不等式推廣定理
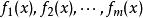閔可夫斯基不等式
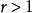閔可夫斯基不等式定理 設 是[a,b]上正的可積函式， ，則：
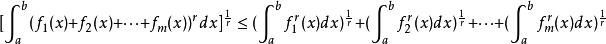閔可夫斯基不等式
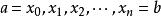閔可夫斯基不等式
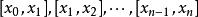閔可夫斯基不等式
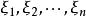閔可夫斯基不等式證明 由假設知所涉及的積分都是可積的，將區間[a,b]n等分， ，得到n個子區間 ，在每個子區間上分別任取一點，分別為 ，則：
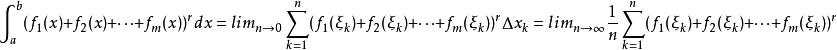閔可夫斯基不等式
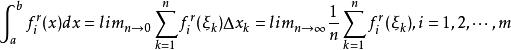閔可夫斯基不等式由閔可夫斯基不等式知：
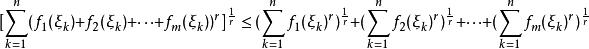閔可夫斯基不等式因此有：
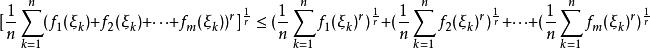閔可夫斯基不等式
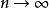閔可夫斯基不等式令 ，由函式的可積性得：
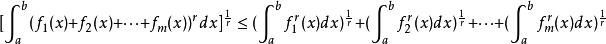閔可夫斯基不等式證明完畢。
