定義
在數學的拓撲學中, 閉映射是兩個拓撲空間之間的映射,使得任何閉集的像都是閉集。所以 f: X→ Y是閉映射,如果 X中的閉集在 f下的像都為 Y的閉集。
閉映射的定義中,並不要求映射連續。與之比較,映射 f: X→ Y為連續映射的定義,是所有 Y的開集的原像為 X的開集,也可等價地定義為所有 Y的閉集的原像為 X的閉集。雖然閉映射的定義,似較連續映射為自然,但在拓撲學中其重要性不及連續映射。
閉映射的概念是由赫維茨(Hurewicz, W.)於1926年,亞歷山德羅夫(Aoexcannpon, I1. C.)於1927年分別引人的。
例子
(1)定義連續函式 f: R→ R為 f( x)= x,則 f是閉映射,但不是開映射。
(2)任何同胚都是既開且閉及連續的。任何雙射的連續映射是同胚,若且唯若映射是開映射,或等價地,若且唯若映射是閉映射。
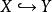 閉映射
閉映射(3) X上的恆等映射是一個同胚,故為既開且閉的。但如果 X是 Y的子空間,則僅當 X在 Y中為閉集時,從 X到 Y的包含映射 是閉映射。故此映射的到達域需要指明,以辨別映射是否為閉映射。
(4)定義從[0,2π)到單位圓(視為 R中的圓,原點為圓心)的函式:在[0,2π)中的θ所對應的值,是單位圓上與 x軸成角度θ的點。這個函式是雙射連續的,所以其從單位圓到[0,2π)的逆函式是既開且閉的。這個逆函式將緊緻的單位圓,映射到不是緊緻的區間[0,2π)。因此可見閉映射不保持緊緻性,這點與連續映射不同。
(5)若 Y有離散拓撲,則任何到 Y中的映射都是既開且閉,但這映射未必連續。例如從實數集 R到整數整 Z的取整函式是既開且閉,但不是連續。
(6)對於任何拓撲空間的積 X= Π X,由積拓撲的定義,其投射 p: X→ X是開且連續的。不過這投射不一定是閉的:例如令 p: R→ R是從 R到 x軸上的投射,並設 A是函式 f( x)=1/ x的圖像,即由全部形如( x,1/ x)的點構成的集合。那么 A是 R中的閉集,但 p( A)不是 x軸中的閉集。不過若 Y為緊緻集,則投射 X× Y→ X是閉映射。
性質
(1)一個映射 f: X→ Y是開映射若且唯若對 X中每一點 x及其任何(任意小的)鄰域 U,都存在 f( x)的鄰域 V使得 V⊂ f( U)。因此若 f將 X的某個拓撲基中的元素都映射到 Y的開集,則 f是開映射。
(2)閉映射的定義,可用內部運算元和閉包運算元表達如下:
設 f: X→ Y是映射, f是閉映射,若且唯若對任何 A⊆ X,有 f( A) ⊆ f( A)。
(3)兩個閉映射的複合是閉映射,
(4)兩個閉映射的積未必是閉映射。(例如取前述的投射 p: R→ R,視之為兩個映射 f和 g的積,其中 f是 x軸上的恆等函式, g是從 y軸到只包含點0的集合{0}的函式。 f和 g為閉映射,但 p不是。)
(5)一個雙射是開的若且唯若其為閉的。一個連續的雙射,其逆映射是雙射的既開且閉映射,反之亦然。
(6)一個滿射的開映射不一定是閉映射,同樣一個滿射的閉映射也不一定是開映射,
(7)設 f是連續映射,且是開的或閉的,那么
•若f是滿射,則f是商映射。
•若f是單射,則f是拓撲嵌入。
•若f是雙射,則f是同胚。
(8) f為開或閉映射的條件,對前兩項只是充分條件,對第三項也是必要條件。
特徵定理
閉映射引理
有些條件能協助辨別映射是否開或閉。以下列出一些這一類的定理。
閉映射引理指,從緊緻集 X到豪斯多夫空間 Y的連續映射 f: X→ Y都是閉且逆緊(緊緻集的原像都為緊緻)。這結果的一個變化指,局部緊緻豪斯多夫空間之間的一個連續映射若為逆緊,則這映射是閉映射。
拓展
泛函分析中的開映射定理指,巴拿赫空間之間的連續線性運算元若是滿射,則為開映射。
複分析中的開映射定理指,在複平面的連通開子集上定義的非常數全純函式是開映射。
區域不變性定理指,兩個 n維拓撲流形間的局部單射且連續的映射都是開映射。