定義
 本質映射
本質映射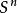 本質映射
本質映射 本質映射
本質映射 本質映射
本質映射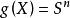 本質映射
本質映射 本質映射
本質映射設為緊空間X到m維球面 的映射,關於與同倫的任意映射 ,有 成立時, 稱為 本質 的 (essential)映 射,否則稱為 非本質的(inessential)映射。非本質映射與“同倫於常值映射”二者是等價的 。
單位圓中的本質映射
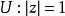 本質映射
本質映射 本質映射
本質映射 本質映射
本質映射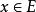 本質映射
本質映射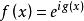 本質映射
本質映射 本質映射
本質映射定義設E是距離空間,我們稱E到單位圓的連續映射是 非本質的,如果存在E到R的連續映射使得對每個都有。E到U的一連續映射稱為 本質的,如果它不是非本質的。(以下所有結論的證明見參考資料) 。
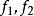 本質映射
本質映射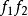 本質映射
本質映射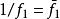 本質映射
本質映射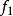 本質映射
本質映射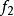 本質映射
本質映射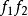 本質映射
本質映射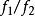 本質映射
本質映射1. 若都是E到U的非本質映射,則與也是非本質的:若是本質的而是非本質的,則與都是本質的。
 本質映射
本質映射 本質映射
本質映射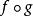 本質映射
本質映射2. 若是E到U的非本質映射,是距離空間F到E的連續映射,則是非本質的。
這些性質都是定義的直接的結果。
 本質映射
本質映射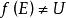 本質映射
本質映射3. 距離空間E到U的任意連續映射,只要,就是非本質的。
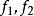 本質映射
本質映射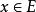 本質映射
本質映射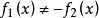 本質映射
本質映射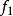 本質映射
本質映射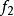 本質映射
本質映射4. 若是距離空間E到U的兩個連續映射並使得對任意都有,又若是本質的(相應地,非本質的),則也是本質的(相應地,非本質的)。
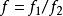 本質映射
本質映射因為,是E到U的連續映射且不取-1,於是據3它是非本質的。
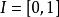 本質映射
本質映射 本質映射
本質映射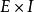 本質映射
本質映射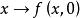 本質映射
本質映射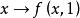 本質映射
本質映射5. 設E是一緊距離空間,,是到U的連續映射,若映射是本質的(相應地,非本質的),則映射也是本質的(相應地,非本質的)。
 本質映射
本質映射 本質映射
本質映射6. (中)一閉球到U的任何連續映射都是非本質的。
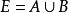 本質映射
本質映射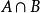 本質映射
本質映射 本質映射
本質映射 本質映射
本質映射 本質映射
本質映射7. 設A,B是距離空間E的兩個閉子集,並且與是連通的,設是E到U的連續映射;若到A與B上的限制都是非本質的,則也是非本質的。
 本質映射
本質映射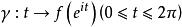 本質映射
本質映射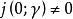 本質映射
本質映射8. 要U到它自身的連續映射為本質的,其充要條件是:對於閉路有。
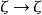 本質映射
本質映射9. U到它自身的恆等映射是本質的 。
本質映射與本質映射定理
 本質映射
本質映射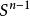 本質映射
本質映射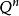 本質映射
本質映射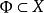 本質映射
本質映射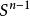 本質映射
本質映射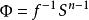 本質映射
本質映射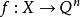 本質映射
本質映射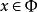 本質映射
本質映射 本質映射
本質映射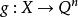 本質映射
本質映射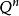 本質映射
本質映射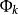 本質映射
本質映射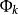 本質映射
本質映射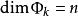 本質映射
本質映射維數論中主要定理之一是所謂 本質映射定理(theorem on essential mappings),它是這一理論重要部分的基礎。設是從(正規)空間X到以 為邊界的n維球上的連續映射,設 是在這個映射之下球面 的原象,。映射稱為 本 質的(essatial),如果在所有點上與一致的每個連續映射都是到整個球上的映射。著名的Aleksandrov theorem定理說,正規空間X有維數dimX≥n,若且唯若X可被本質地映射到一個n維球上。由這個定理可以得出和定理(對於緊統,在維數論發展初期已由Menger等給出證明):如果維數dimX=n的(正規)空間X是有限或可數多個閉子集的並,則這些中至少有一個滿足。
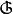 本質映射
本質映射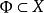 本質映射
本質映射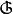 本質映射
本質映射關於本質映射的定理是所謂的同調維數論(homologicaldimension theory)的基礎,它使我們能套用代數拓撲的方法在更為一般的假設下研究維數。空間的同調維數(homological dimension of a space)的概念與閉鏈和同調的概念有關,因此假定,與拓撲空間X同時還給定一個交換群,稱之為係數群。於是可以談論具有這個係數群的緊統X的閉鏈,它們的支撐,特別是談論X中關於係數域同調於零的閉鏈 。

