概念
可擴映射(expansive map)是一類重要的動力系統。設(M,d)是一個度量空間,f:M→M是一連續映射,如果存在常數ζ>0,使得對任意x,y∈M,x≠y,存在n≥0,滿足d(f(x),f(y))≥ζ,那么就稱f是可擴映射。這時,ζ被稱為是f的一個可擴常數。該定義的等價說法之一是:如果存在常數ζ>0,滿足:
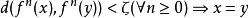 可擴映射
可擴映射那么就稱f是可擴映射。當f:M→M是同胚,而且允許上述定義的n在整數範圍內取值時,就稱f是可擴同胚。擴張映射是可擴映射。微分同胚在其雙曲不變集上的限制是可擴同胚,特別地,安諾索夫微分同胚是可擴同胚。
度量空間
度量空間亦稱距離空間。一種拓撲空間,其上的拓撲由距離決定。設R是一個非空集合,ρ(x,y)是R上的二元函式,滿足如下條件:
1.ρ(x,y)≥0且ρ(x,y)=0⇔x=y;
2.ρ(x,y)=ρ(y,x);
3.(三角不等式)ρ(x,y)≤ρ(x,z)+ρ(y,z);
則稱ρ(x,y)為兩點x,y之間的距離,R按距離ρ成為度量空間或距離空間,記為(R,ρ)。設A是R的子集,則A按R中的距離ρ也成為度量空間,稱為R的(度量)子空間。如果把上述距離的條件1改為ρ(x,y)≥0且ρ(x,x)=0,則稱ρ為R上的擬距離。當ρ(x,y)=0時,記x~y。~是R上的一個等價關係,記商集(即等價類全體)為D=R/~,在D上作二元函式ρ~:ρ~(x~,y~)=ρ(x,y)(x∈x~,y∈y~),則ρ~是D上的距離,而(D,ρ~)稱為R按擬距離ρ導出的商(度量)空間。
度量空間(R,ρ)中的子集A稱為有界的,如果對x∈R,存在常數M,使ρ(x,x)≤M對A中的一切x成立。設x∈R,r>0,則稱集合{x|x∈R,ρ(x,x)<r}為以x為中心,r為半徑的開球,或x的r鄰域,記為O(x,r)。又設A⊂R,若對任何x∈A,存在x的某個鄰域O(x,r)⊂A,則A稱為開集;而稱開集的補集為閉集.R中包含子集A的最小閉集就稱為A的閉包。
度量空間是弗雷歇(Fréchet,M.-R.)於1906年引進的,它是現代數學中的一種基本而重要並且非常接近於歐幾里得空間的抽象空間,也是泛函分析的基礎之一。
連續映射
設f為從拓撲空間E到拓撲空間F中的映射。稱f在E的點x0是連續的,如果對f(x)在F中的任一鄰域W,在E中存在x0的鄰域V,使在f下V的象包含在W中;換言之,如果在f下f(x0)的任一鄰域的逆象是x0的鄰域。
稱f在E上是連續的(或簡稱f是連續的),如果它在E的每一點都連續。
為使f是連續的,必須且只須F的任一閉集經由f的逆象是E的閉集,或F的任一開集經由f的逆象是E的開集. 但是E的開集(閉集)經由連續映射的正象不一定是F的開集(閉集)。
從E到F中的常映射是連續的.E的恆等映射是連續的。
任一從離散空間到拓撲空間的映射是連續的。
設E,F及G為拓撲空間,f為從E到F中的連續映射,而g為從F到G中的連續映射,則複合映射g°f是連續的.
當E與F為分別賦以距離d及e的度量空間時,為使f在x0點連續,其充分必要條件是:對任一嚴格正的實數ε,存在嚴格正的實數η,使得由關係d(x0)≤η可推出e(f(x),f(x0))≤ε.若f為定義在R的子集P上的有限數值函式,則使f在x0點連續的充分必要條件是:對任一嚴格正的實數ε,存在嚴格正的實數η,使得對P的任一元素x,關係|x-x| ≤η蘊涵:|f(x)-f(x0)|≤ε。
同胚的概念
同胚是拓撲空間之間的一種變換。若f是拓撲空間(X,T)到(Y,U)的單滿映射,並且f與f都是連續的,則稱f為同胚映射或拓撲變換。存在同胚映射的兩個拓撲空間稱為同胚的或拓撲等價的.同胚關係是等價關係。抽象空間的同胚是弗雷歇(Fréchet,M.-R.)於1910年開始研究的.在狹窄的意義下同胚的概念早已被龐加萊(Poincaré,(J.-)H.)引入。
設E與F為兩個拓撲空間。稱從E到F上的雙射為從E到F上的同胚,如果這一映射能建立一個從E之全體開集的集合到F之全體開集的集合上的雙射。
為使從E到F上的雙射是同胚,其充分必要條件是: 這個雙射是雙連續的。
從一緊空間到另一緊空間上的任一連續雙射是同胚。
微分同胚
 可擴映射
可擴映射 可擴映射
可擴映射微分同胚是微分流形之間的一類同胚映射。它與它的逆映射都是可微的。設M,N均為微分流形,對於映射f:M→N,若f是同胚映射,並且f,f都是C可微映射,則稱f為M到N上的C微分同胚。C微分同胚f:M→N簡稱M到N上的微分同胚.對於微分流形M,N,若存在(C)微分同胚f:M→N,則稱M與N是(C)微分同胚的微分流形,記為MN。“”是微分拓撲學中的基本等價關係。微分拓撲的基本任務是研究微分流形在微分同胚下保持不變的性質,以及尋求在怎樣的條件下兩個微分流形是微分同胚的。米爾諾(Milnor,J.W.)於1956年證明,在S上至少存在兩個不微分同胚的微分構造.後來證實,S上恰好有15個這樣的不同的微分構造。
設E與F為R或C上的兩個賦范向量空間,U,V分別為E與F的開集. 稱從U到V中的映射f是(C類的)微分同胚,如果這個映射本身及其逆映射都是雙射,而且是連續可微的。
設p為大於1的整數。稱f是Cp-微分同胚,如果f及其逆映射都是雙射,而且是Cp類的映射。為使微分同胚f是Cp-微分同胚,只須f是C類的。
C∞-微分同胚的定義可同樣給出。
