定理定義
 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理設X,Y為巴拿赫空間,T:X Y為線性運算元。定義T的圖像為 的子空間
 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理Γ(T)={(x,T(x)) ,x X}。
 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理賦予 範數║(x,y)║=║x║+║y║使得 成為巴拿赫空間。那么,這定理指T是連續的(與有界等價)若且唯若Γ(T)在 內是閉集。
驗證推導
閉圖像定理可以從開映射定理推導出來。
 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理Γ(T)是閉集的充分必要條件是如果序列{(x,y)}包含於Γ(T)(即對任意n有y=T(x)),而(x,y) (x,y),那么(x,y) Γ(T),y=T(x)。如果T是連續的,從連續性立刻可知Γ(T)是閉集,因為連續性是更強的條件:如果x x,則T(x) T(x)。
如果Γ(T)是閉集,可以在Γ(T)定義線性運算元
 閉圖像定理
閉圖像定理π:Γ(T) X,x是(x,y)的一個逆像,
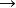 閉圖像定理
閉圖像定理π:Γ(T) Y,y是(x,y)的一個逆像。
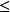 閉圖像定理
閉圖像定理顯然║π(x,y)║=║y║ ║(x,y)║,因此π是有界運算元。
 閉圖像定理
閉圖像定理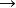 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理Γ(T)是巴拿赫空間X Y中的閉子空間,所以Γ(T)是巴拿赫空間。X也是巴拿赫空間,π是雙射,從而由開映射定理的系可知,其逆π :X Γ(T)為有界運算元,因為T=π π ,故T也是有界的。
定理推廣
從這定理可得出黑林格-特普利茨定理──希爾伯特空間上處處定義的對稱線性運算元是有界的。
泛化
閉圖像定理可以通過以下方式推廣到更抽象的拓撲向量空間:
若且唯若其圖形在配備產品拓撲的X×Y空間中被關閉時,從圓筒空間X到Fréchet空間Y的線性運算符是連續的。
並且有一個不需要Y局部凸的版本:
如果兩個F空間之間的線性映射圖被關閉,則映射是連續的。
而閉圖像定理的一般版本是:
 閉圖像定理
閉圖像定理 閉圖像定理
閉圖像定理假設X和Y是兩個拓撲向量空間(它們不需要是Hausdorff或局部凸起),具有以下屬性:如果G是 任何閉合子空間,而y是任何連續映射 的G到X,那么你是一個開放的映射。 在這種情況下,如果 是一個線性映射,其圖形被關閉,則f是連續的。

