簡介
巴拿赫逆運算元定理是關於有界逆運算元存在的定理。
設X,Y為弗雷歇空間,T是(T)⊂X到(T)⊂Y的閉線性運算元,如果T是一對一的,且(T)是Y中的第二範疇集,則T 是定義在Y上的連續線性運算元。
特別地,從巴拿赫空間X到巴拿赫空間Y上的一對一有界線性運算元T的逆T 是定義在Y上的有界線性運算元。
有界線性運算元
有界線性運算元是泛函分析中一種重要的運算元。
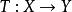 巴拿赫逆運算元定理
巴拿赫逆運算元定理 巴拿赫逆運算元定理
巴拿赫逆運算元定理 巴拿赫逆運算元定理
巴拿赫逆運算元定理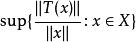 巴拿赫逆運算元定理
巴拿赫逆運算元定理 巴拿赫逆運算元定理
巴拿赫逆運算元定理 巴拿赫逆運算元定理
巴拿赫逆運算元定理 巴拿赫逆運算元定理
巴拿赫逆運算元定理 巴拿赫逆運算元定理
巴拿赫逆運算元定理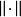 巴拿赫逆運算元定理
巴拿赫逆運算元定理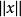 巴拿赫逆運算元定理
巴拿赫逆運算元定理 巴拿赫逆運算元定理
巴拿赫逆運算元定理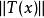 巴拿赫逆運算元定理
巴拿赫逆運算元定理 巴拿赫逆運算元定理
巴拿赫逆運算元定理設是從線性賦范空間到的線性運算元。 如果當存在且有限,則稱是有界線性運算元,也就是說將中的每個有界集映射為中的有界集。此處|表示範數,表示中定義的範數,表示中定義的範數。
閉線性運算元
(closed linear operator)
閉線性運算元是一種特殊的線性運算元,常直接稱為閉運算元。連續線性運算元必是閉運算元,但閉運算元不一定是連續運算元。根據閉圖像定理可知,定義域是閉子空間的閉運算元是連續運算元。
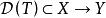 巴拿赫逆運算元定理
巴拿赫逆運算元定理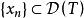 巴拿赫逆運算元定理
巴拿赫逆運算元定理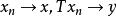 巴拿赫逆運算元定理
巴拿赫逆運算元定理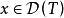 巴拿赫逆運算元定理
巴拿赫逆運算元定理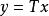 巴拿赫逆運算元定理
巴拿赫逆運算元定理設X,Y均為Banach空間,T是的線性運算元。對於任意的,若由可得,且,則稱T為 閉線性運算元,簡稱 閉運算元。
