定義
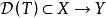閉線性運算元
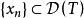閉線性運算元
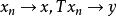閉線性運算元
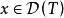閉線性運算元
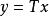閉線性運算元定義1（閉線性運算元）設X，Y均為Banach空間，T是 的線性運算元。對於任意的 ，若由 可得 ，且 ，則稱T為閉線性運算元，簡稱閉運算元。
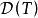閉線性運算元 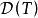閉線性運算元註：每個連續線性運算元T都可以將定義域 延拓到 的閉包上，因此每個連續線性運算元T都可以看成是有閉定義域的，於是每個連續線性運算元必是閉運算元；但一般的閉線性運算元不一定是連續運算元（下面的例1證實了這一說法）。
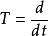閉線性運算元
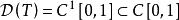閉線性運算元
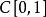閉線性運算元
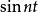閉線性運算元例1考察微分運算元 ，它是定義在 上，取值於 的線性運算元。取函式 ，則
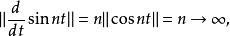閉線性運算元
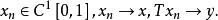閉線性運算元
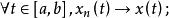閉線性運算元因此T是無界運算元，從而不是連續運算元。下證T是閉運算元。設 則對 另一方面，
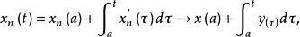閉線性運算元所以，
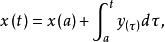閉線性運算元
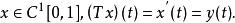閉線性運算元故
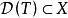閉線性運算元定義2（線性運算元的圖像）令T是定義在 上到Y的線性運算元，稱
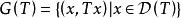閉線性運算元為T的圖像。
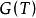閉線性運算元
閉線性運算元註： 是 的線性子空間。
性質
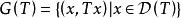閉線性運算元 閉線性運算元上面定義的閉線性運算元有一個重要性質，即T的圖象 為乘積空間 的一個閉線性子空間。定理描述為：
閉線性運算元定理1 T是閉運算元的充分必要條件是 為閉集。
閉線性運算元
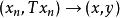閉線性運算元 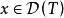閉線性運算元 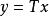閉線性運算元
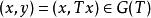閉線性運算元 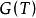閉線性運算元證明：（1）必要性 設 ， . 因為T是閉運算元，則 ， ，於是 ，故 是閉集。
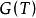閉線性運算元 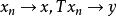閉線性運算元（2）充分性 設 是閉的，若 ，那么
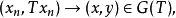閉線性運算元
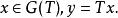閉線性運算元這表明
套用-閉圖像定理
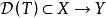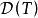閉線性運算元 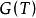閉線性運算元 閉線性運算元 閉線性運算元定理2（閉圖像定理）設X，Y均為Banach空間，T是 的線性運算元。 是X中的閉集。若 是 中閉集，則T是連續的。
證：該定理的證明參見參考文獻[1] 的291-292頁。
由定理1可知，定理2還可敘述成：在定理2的條件下，若T是閉運算元，則T是連續的。因此定義域是閉子空間的閉運算元是連續運算元。
拓展
閉線性運算元原是泛函分析中的概念，後被引入魯棒控制中討論系統的不穩定攝動問題。經研究發現，控制系統中一個對象的傳遞函式P(s)(n×m階實有理矩陣)，若僅在有限功率譜輸入與輸出情況下考慮，實際上等於引入了一個從輸入空間H到輸出空間H的閉線性運算元，這一結論為在魯棒控制中引入隔撲(Gap)概念討論系統的不穩定攝動打下了基礎。
