定理公式
電磁能量一如其他能量服從能量守恆原理,坡印亭定理用來表征電磁場能量守恆關係的。
積分形式的坡印廷定理
對於由閉合曲面 S所限定的體積V,有:
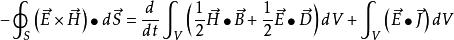 坡印亭定理
坡印亭定理式中: J是電流密度; E是電場強度; H是磁場強度; B是磁感應強度; D電位移矢量
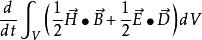 坡印亭定理
坡印亭定理其中: ——在單位時間內體積 V 內所增加的電磁場能量;
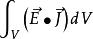 坡印亭定理
坡印亭定理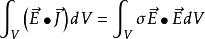 坡印亭定理
坡印亭定理——單位時間內電場對體積V中的電流所做的功,導電媒介中 即為體積V內總的消耗功率。
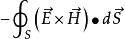 坡印亭定理
坡印亭定理——單位時間內通過曲面進入體積V的電磁能量
所以矢量 Ex H定義為電磁能流密度矢量 S(坡印廷矢量),即
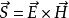 坡印亭定理
坡印亭定理這樣,若已知某點的 E和 H,即可求出該店的能流密度矢量。
這就是電源外區域的、積分形式的坡印亭定理。它的含義是:垂直穿過閉合面S進入體積V的功率,等於體積內電磁儲能的增長率與由傳導電流 J引起的功率損耗之和,更一般的情況是:
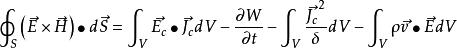 坡印亭定理
坡印亭定理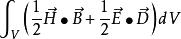 坡印亭定理
坡印亭定理式中 E為電源中的局外場強, J為傳導電流,σ為體積V內介質的電導率,ρ為運動電荷的電荷密度, v為該電荷的運動速度, E= J/σ- E為總場強,W為 。
整個方程的含義是:外源提供的功率等於體積V內電磁能量的增加率、傳導電流的功率損耗、運動電荷作功耗損的功率、垂直穿過曲面A向外界輸送的功率之總和。
微分形式的坡印廷定理
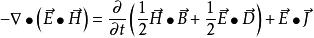 坡印亭定理
坡印亭定理在體積V上,對上式兩端積分,並套用散度定理,即可得到坡印亭定理積分形式。
推導過程
坡印亭定理可由麥克斯韋方程組推導出來。假設閉合面 S 包圍的體積 V 中無外加源,媒質是線性的、各向同性的且參數不隨時間變化。
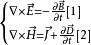 坡印亭定理
坡印亭定理分別用 E 點乘方程[1]、 H 點乘方程[2],得
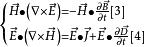 坡印亭定理
坡印亭定理將[3]、[4]兩式相減,得到
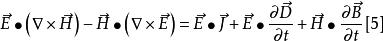 坡印亭定理
坡印亭定理線上性、各向同性的媒質中,當參數不隨時間變化時
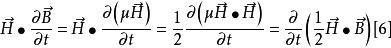 坡印亭定理
坡印亭定理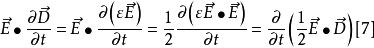 坡印亭定理
坡印亭定理將[6]、[7]式代入[5],於是得到,
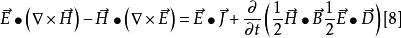 坡印亭定理
坡印亭定理再利用矢量恆等式
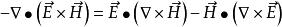 坡印亭定理
坡印亭定理可得到
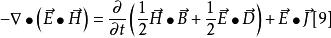 坡印亭定理
坡印亭定理這就是坡印亭定理的微分形式,在體積 V 上,對[9]式兩端積分,並套用散度定理,即可得到
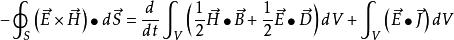 坡印亭定理
坡印亭定理這就是表征電磁能量守恆關係的坡印亭定理
定理影響
 坡印亭定理
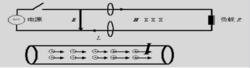
坡印亭定理坡印亭定理給出了時變電磁場能量傳播的一個新圖像,電磁場能量通過電磁場傳播。這對廣播電視、無線通信和雷達等套用領域是不難理解的。
恆定電流或低頻交流電的情況下,場量往往是通過電流、電壓及負載的阻抗等參數表現,表面上給人造成了能量是通過電荷在導線內傳輸的假象。
如果能量真的是通過電荷在導線內傳輸,常溫下導體內的電荷運動速度約為10 m/s,電荷由電源端到負載端所需時間約是場傳播時間的億萬倍。
電磁場能量通過電磁場傳播,負載只需通過極短(t=L/c,其中c為光速)的時間就能得到能量的供應。
