介紹
 鏈式法則
鏈式法則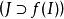 鏈式法則
鏈式法則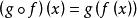 鏈式法則
鏈式法則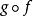 鏈式法則
鏈式法則 鏈式法則
鏈式法則鏈式法則是求複合函式的導數(偏導數)的法則,若 I,J 是直線上的開區間,函式 f(x) 在 I 上有定義 處可微,函式 g(y) 在 J 上有定義 ,在 f(a) 處可微,則複合函式 在 a 處可微 ( 在 I 上有定義),且 . 若記 u=g(y),y=f(x),而 f 在 I 上可微,g 在 J 上可微,則在 I 上任意點 x 有
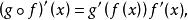 鏈式法則
鏈式法則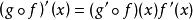 鏈式法則
鏈式法則即 ,或寫出
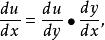 鏈式法則
鏈式法則這個結論可推廣到任意有限個函式複合到情形,於是複合函式的導數將是構成複合這有限個函式在相應點的 導數的乘積,就像鎖鏈一樣一環套一環,故稱鏈式法則。
基本信息
若多元函式 u=g(y,y,...,y) 在點 =(b,b,...,b) 處可微,b=f(a,a,...,a)(i=1,2,...,m),每個函式 f(x,x,...,x) 在點 (a,a,...,a) 處都可微,則函式 u=g(f(x,x,...,x),f(x,x,...,x),...,f(x,x,...,x)) 也在(a,a,...,a) 處可微,且
 鏈式法則
鏈式法則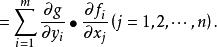 鏈式法則
鏈式法則這就是多元函式的鏈式法則,若同時考察一組(p 個)複合函式 u,u,...,u,其中 u=g(f(x,x,...,x),f(x,x,...,x),...,f(x,x,...,x))(k=1,2,...,p),將它們的偏導數寫成矩陣(雅可比矩陣),則可以看到鏈式法則在形式上更有規律性,這時
 鏈式法則
鏈式法則若對於上面考察的這些函式,令 =(g,g,...,g),=(f,f,...,f),於是, 是 p 維向量值函式(定義與 的子集上), 是 m 維向量值函式(定義於 的子集上),按照定義,它們的導數是相應的雅可比矩陣,
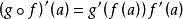 鏈式法則
鏈式法則(等式右端為兩矩陣‘ ( ()) 與‘ () 的矩陣乘積),其中=(a,a,...,a).這就是向量值函式的鏈式法則,它在形式上與一元函式的鏈式法則完全相同。
例題
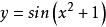 鏈式法則
鏈式法則求導
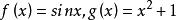 鏈式法則
鏈式法則鏈式求導:令
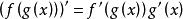 鏈式法則
鏈式法則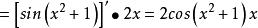 鏈式法則
鏈式法則則即可求得。
 鏈式法則
鏈式法則在實際套用中,可將 看作是分數的約分過程,這種用法在求不定積分中會更廣泛地使用。

