定義
錐面通過一個定點V且與定曲線r(它不過定點V)相交的所有直線構成的曲面稱為 錐面；定點V叫做 頂點。定曲線C叫做錐面的 準線，構成曲面的每一條直線叫做 母線。設錐面的準線 的方程為
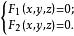錐面
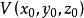錐面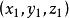 錐面
錐面那么通過頂點 和準線 上一點 的直線即錐面的母線方程是
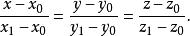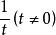錐面
錐面令上式的比值等 而得
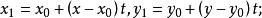錐面
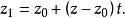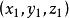錐面 錐面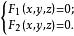 錐面 錐面因 是準線 上的點，故適合式 ，將上式代入，然後再消去t，即得錐面的普通方程。 特別地，如果錐面的頂點為坐標原點，準線為
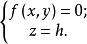錐面那么錐面的方程就是
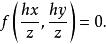錐面事實上，因母線的方程為
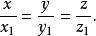錐面又
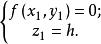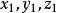錐面
錐面消去 便得
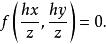錐面定理
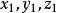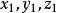錐面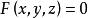 錐面
錐面以原點為頂點的錐面方程是關於 的齊次方程，反之，一個含 的齊次方程 的圖形總是頂點位於原點的錐面。
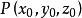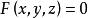錐面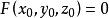 錐面
錐面事實上．設 是曲面 上的一點(但不是原點)。即 ，則直線OP上的任意一點M的坐標為
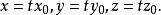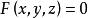錐面 錐面一定也適合方程 ，因為
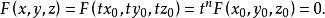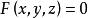錐面 錐面這裡的n是所給齊次方程的次數，這表示直線OP上任意一點都在曲面 上，因此該曲面是由過原點的直線構成的，根據定義，這曲面是以原點為頂點的錐面。
例題
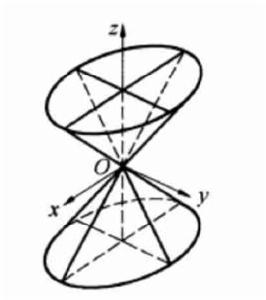
求以原點為頂點，以橢圓
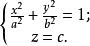錐面為準線的錐面(圖1)的方程。
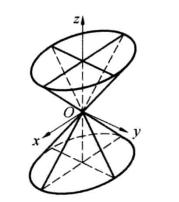圖1解 據式
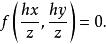錐面知，所求錐面的方程是
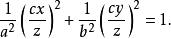錐面即
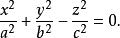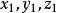錐面 錐面這是關於 的二次齊次方程，這錐面叫做二次錐面，當a=b時，就是圓錐面。
