費因曼圖
正文
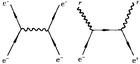費因曼圖在量子場論微擾論中所用的一種圖解法。在量子場論中，系統的總哈密頓量Hi（能量算符）包括自由場哈密頓量Hf和相互作用哈密頓量Hi兩部分：H=Hf+Hi。忽略各場之間相互作用時的哈密頓量稱為自由場哈密頓量Hf，而場之間的相互作用由相互作用哈密頓量Hi來描述。Hi中包含一個係數，稱為耦合常數，它描述這種相互作用的強弱程度。由Hi可構成S 矩陣,與具體物理過程的初末態相聯繫的S 矩陣元決定著這一特定物理過程的躍遷幾率。在S 矩陣元中，提出一個反映由初態向末態轉化過程中能量動量守恆的因子δ4(∑p)後，便得到M矩陣元,具體物理過程的躍遷幾率直接與|M|2成比例。一個重要而又困難的問題是建立一種計算方法，去具體計算各種反應的M矩陣元。在量子電動力學中，Hi的耦合常數就是電荷e，它的二次方給出精細結構常數α＝2πe2/(hс)≈1/137。M矩陣可以按電荷e展開，
而且因為α很小，如果Mn不無限增大，那么只要計算前幾項就足以描寫反應過程了。這種計算方法稱為微擾論。
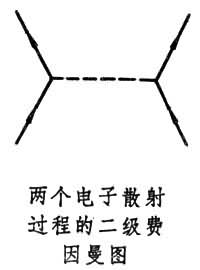
R.P.費因曼提出一種圖解方法（即費因曼圖），把M矩陣的每一項都與一定的費因曼圖聯繫起來，由確定的圖，可以根據費因曼規則，很快地寫出相應矩陣元的表達式，而且由費因曼圖可以清楚地得出這過程的物理解釋。在量子電動力學中，在費因曼圖里用一根帶箭頭的實線代表電子，帶反箭頭的實線代表正電子，虛線代表光子，電子、正電子和光子的每一次相互作用都用交於一點的兩根實線（箭頭分別指向和指離交點）和一根虛線來描寫，這交點稱為作用頂點。代表初態或末態的線只有一頭連線頂點，稱為外線，而介於兩個頂點之間的線稱為內線，內線描寫傳遞相互作用的中間過程的粒子，稱為虛粒子。在任一費因曼圖中，沿實線箭頭方向移動，實線或者聯成圈，或者由外線引向另一外線，它不會在任一頂點終止，這反映了在反應過程中電子數是守恆的。費因曼圖的頂點數目稱為費因曼圖的級數，n級費因曼圖代表M矩陣展開式中Mn的一項。例如兩個電子的散射過程，它的二級費因曼圖，如圖所示，它描寫一個電子先放出一個光子，這帶有一定能量動量的光子傳遞到另一電子，並被後一電子所吸收。這樣，兩個電子的電磁散射，不是它們的直接作用，也不是超距作用，而是由電子場與電磁場的相互作用，通過發射和吸收光子的過程來實現的。作為中間過程的光子，它被發射以後很快被第二個電子所吸收，它與可以被實驗儀器直接觀測到的物理光子不同，稱為虛光子。利用費因曼發展起來的這套方法，可以系統而方便地計算各種電磁過程幾率，而且物理意義十分明確。這種方法也可以用於其他量子場論。
費因曼圖