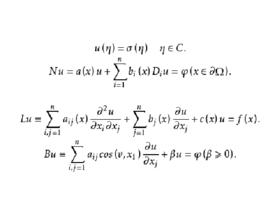概括
套用領域
最早研究的邊值問題是狄利克雷問題,是要找出調和函式,也就是拉普拉斯方程的解,後來是用狄利克雷原理找到相關的解。物理學中經常遇到邊值問題,例如波動方程等。許多重要的邊值問題屬於Sturm-Liouville問題。這類問題的分析會和微分運算元的本徵函式有關。在實際套用中,邊值問題應當是適定的(即,存在解,解唯一且解會隨著初始值連續的變化)。許多偏微分方程領域的理論提出是為要證明科學及工程套用的許多邊值問題都是適定問題。在微分方程中,邊值問題是一個微分方程和一組稱之為邊界條件的約束條件。邊值問題的解通常是符契約束條件的微分方程的解。
分類
根據條件的形式,邊值條件分以下三類:
①第一類邊值條件:也稱為狄利克雷邊界條件,直接描述物理系統邊界上的物理量,例如振動的弦兩端與平衡位置的距離;
②第二類邊值條件:也稱為諾伊曼邊界條件,描述物理系統邊界上物理量垂直邊界的導數的情況,例如導熱細桿端點的熱流;
③第三類邊值條件:物理系統邊界上物理量與垂直邊界導數的線性組合,例如,細桿端點的自由冷卻,溫度、熱流均不確定,但是二者的關係確定,即可列出二者線性組合而成的邊值條件。
狄利克雷問題
概念
許多數學物理問題可以化為根據區域邊界上的已知值作出在區域內的調和函式,這類問題稱為狄利克雷問題。
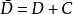 邊值問題
邊值問題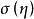 邊值問題
邊值問題求出一個在區域D內調和並且在 上連續的函式u(z),使它在C上取已知值 :
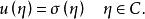 邊值問題
邊值問題例如,在某區域內求流體(無源、無旋)的速度或靜電場(無電荷)的電位,當這區域邊界上的速度或電位已經知道時,這便是狄利克雷問題。
唯一性定理
先來證明狄利克雷問題的解的唯一性定理:
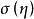 邊值問題
邊值問題定理1 在已知區域D,對於給定的邊界值 ,狄利克雷問題的解不能多於一個。
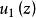 邊值問題
邊值問題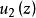 邊值問題
邊值問題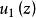 邊值問題
邊值問題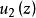 邊值問題
邊值問題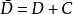 邊值問題
邊值問題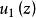 邊值問題
邊值問題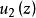 邊值問題
邊值問題 邊值問題
邊值問題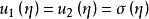 邊值問題
邊值問題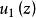 邊值問題
邊值問題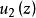 邊值問題
邊值問題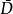 邊值問題
邊值問題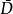 邊值問題
邊值問題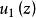 邊值問題
邊值問題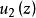 邊值問題
邊值問題 邊值問題
邊值問題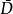 邊值問題
邊值問題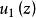 邊值問題
邊值問題 邊值問題
邊值問題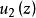 邊值問題
邊值問題證明 假設 與 是狄利克雷問題的兩個解,則 - 在區域D內調和,在 上連續,沿C, - 0,(因沿C, )由定理2, -在 上的最大值與最小值兩個都等於零,因而在 上, - 0;由此可見,在 上 ,於是定理得證。
定理2一個在區域D內不為常數的調和函式,不可能在這區域的內點達到最大值或最小值。
斜微商問題
求解滿足斜微商邊界條件的橢圓型方程的解的問題,形如
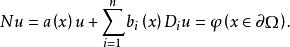 邊值問題
邊值問題的邊界條件稱為斜微商邊界條件,若向量b=(b,b,…,b)的法向分量b在∂ Ω上非零,則稱上述條件為正則斜微商邊界條件。
第三邊值問題
對二階橢圓型方程求邊界上解與其法嚮導數的線性組合為已知的解,設Ω為R中的有界域,求在Ω中滿足方程
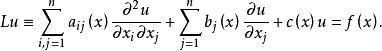 邊值問題
邊值問題在閉域Ω-上連續,在Ω的邊界Γ上滿足條件
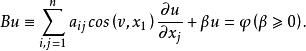 邊值問題
邊值問題的解的問題稱為第三邊值問題或者魯賓問題,這裡ν為外法線,如果c(x)≤0且c與β不都恆為0,那么第三邊值問題的解是惟一的。特別地,拉普拉斯方程的第三邊值問題:在Ω中Δu=0,在Γ上
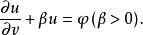 邊值問題
邊值問題的解唯一。