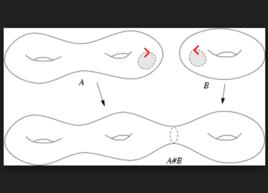
點上的連通和
兩個 m維流形的 連通和為一流形,其將兩個流形各挖去一個球,再將球面邊界黏在一起。
若兩個流形是可定向的,由逆轉定向黏合映射定義的連通和是惟一的。即使這建構使用到的球的選擇,但最後結果都會於同胚下統一。亦可以將此運算作用於光滑範疇上,而其結果也會於微分同胚下統一。
連通和的運算標記為#;例如,A#B即表示為 A和 B的連通和。
連通和的運算中有一球面S 為單位元;亦即,M#S 會同胚(或微分同構)於 M。
閉球面的分類,在拓撲學上的一基本及重大結果,其描述為:任一閉曲面均可表示成 g個環面和 k個實射影平面的連通和。
子空間內定義
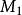 連通和
連通和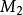 連通和
連通和 連通和
連通和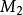 連通和
連通和設和為兩個光滑、可定向且相同維度的流形,及 V為一光滑、封閉且可定向的流形,可內嵌成和的子流形。此外,再假設其存在一法叢的同構
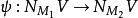 連通和
連通和其將每一纖維的定向顛倒。然後,ψ便可導出一定向保留的微分同構
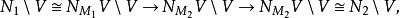 連通和
連通和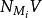 連通和
連通和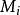 連通和
連通和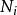 連通和
連通和其中,每一法叢都會微分同構地和於內 V的鄰域一致,且映射
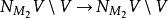 連通和
連通和